[科普中国]-傅里叶一比当定理

傅里叶-比当定理(Fourier-Budan theorem)是关于实系数多项式在确定区间内根的个数的一个命题，该定理断言：设f(x)是一个实系数n次多项式，如果f(a)≠0，f(b)≠0，a x0时这序列没有变号(当x充分接近x0)。

现假设点x通过多项式f(m)的r重根x0,而x0不是多项式f(m-1)的根(这时x0可以是f的根,也可以不是f的根)，只要证,通过点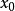时序列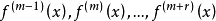的变号次数改变一个非负偶数，在点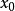的邻域这些多项式分别接近于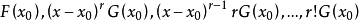。如果除去，则当xx0时没有变号。

再讨论开头两项，与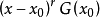，当r为偶数时，对xx0变号次数相同，而当r为奇数时，对xx0的变号次数多1或少1(依赖于与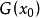同号或异号)，因此对偶数r，变号次数等于r，对奇数r，变号次数等于r±1，在两个情形这个变号次数都是非负偶数2。

相关推论推论1(Descartes法则) 多项式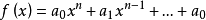的正根个数不超过序列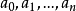的变号次数2。

证明 因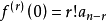，故N(0)与多项式f的系数序列的变号次数相同。又显然N(+∞)=0，

附注：Jacobi证明了Descartes 法则可用来估计在α与β之间的根的个数。

为此需要作变换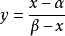,即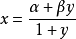，又考察多项式

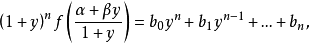应用Decartes法则到这多项式，给出在α与β之间的根的个数的估值，事实上，当x由α变至β时，y由0变至∞。

推论2(de Gua) 如果多项式缺少相继的2m个项(即这些项的系数等于零)，则这多项式至少有2m个虚根，又如果缺少2m+1个相继的项，则当包含它们的项异号时多项式至少有2m个虚根，而当包含它们的项同号多项式至少有2m+2个虚根。

在某些情况下，比较两个序列的变号次数可得到的根个数比Fourier- Budan定理所给出的更准确估值，这种定理首先由Newton表述，但只是到Sylvester在1871年才证明。

定理(Newton-Sylvester) 设f内无重根的多项式，则多项式f在a与b之间(其中a