[科普中国]-自旋－轨域耦合

自旋－轨域耦合是粒子的自旋与轨道动量的相互作用引起的轨道能级上的“细小”分裂。最典型的例子是电子能级的位移。电子移动经过原子核的电场时，会产生电磁作用，电子的自旋与这电磁作用的耦合，形成了自旋-轨域作用。谱线分裂实验明显地侦测到电子能级的位移，证实了自旋-轨域作用理论的正确性。另外一个类似的例子是原子核壳层模型能级的位移。半导体或其它新颖材料常常会涉及电子的自旋－轨域耦合效应。自旋电子学专门研究与应用这方面的问题1。

概述我们知道，电场对静止的电荷有静电力的作用，电场对运动的电荷除了有静电力的作用外还有磁场力的作用。磁场对静止的电荷没有力的作用，磁场对运动的电荷有力的作用。电场对静止磁矩无相互作用，电场对运动磁矩有力矩作用。自旋－轨域耦合的本质是外电场对运动自旋磁矩的作用，自旋－轨域耦合同时也是一个相对论的效应。

如图（a）表示的是原子核坐标系，根据库仑定律，原子核在运动电子－e处产生一电场，电子绕原子核以速度v运动，存在一自旋磁矩，场对运动的磁矩将会产生相互作用，所以该自旋磁矩和由原子实在该处产生的电场将产生相互作用，这就是自旋轨道互作用的起源。由于运动是相对的，上述运动也可以看成电子不动，原子核绕电子运动，如图（b），对应的自旋－轨域耦合则可以理解成电子是静止的，电场E以－v运动产生一个磁场B，这磁场B对自旋有力矩的作用。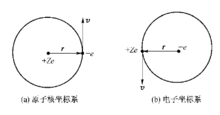

自旋是相对论量子力学的自然结果，所以更严格地给出原子中自旋－轨域耦合必须要从狄拉克方程出发，通过狄拉克方程的非相对论极限可以得出自旋－轨域耦合的具体形式2。

理论发展自旋－轨域耦合是指耦合电子的自旋自由度和它的轨道自由度之间的关系，这种关系提供了一种新的方式来控制电子自旋，即人们可以方便地用外加电场或门电压来控制和操纵电子的自旋，进而实现自旋电子器件。

自旋－轨域耦合在半导体自旋电子学有很多具体应用，实际研究中根据介质材料所受力的性质和材料结构对称性可以将自旋－轨域耦合分为Rashba自旋－轨域耦合和Dressalhaus自旋－轨域耦合。

Rashba自旋－轨域耦合相互作用机制是由Rashba首先引入的，Rashba自旋－轨域耦合起源于结构反演不对称，材料结构的非中心对称性将导致能带倾斜。

在三维晶体环境中，势能起源于晶体周期势。大多数多元半导体具有闪锌矿晶格结构或者铅锌矿晶格结构，二者都没有反演对称性。Dresselhaus证明了这种体反演不对称性质会导致导带有一个自旋－轨域耦合引起的劈裂而形成两个子带2。

应用意义随着自旋电子学的迅猛发展，自旋－轨域耦合越来越受到人们的广泛关注，国际上关于相关材料中自旋－轨域耦合引起的各种新奇物理现象的报道越来越多，如自旋霍尔效应、自旋场效应晶体管、低损耗的自旋、自旋量子计算等。自旋－轨域耦合作用提供了一种全电学（不需要外磁场或磁性材料）的方法控制自旋，随着理论研究的深入和实验技术的发展，基于自旋－轨域耦合的各种电子器件层出不穷，也必将会带来更大的实际应用价值1。

本词条内容贡献者为:

程鹏 - 副教授 - 西南大学