欧几里得定理是数论中的基本定理,定理指出素数的个数是无限的。该定理有许多著名的证明。
欧几里得的证明欧几里得在他的著作《几何原本》(第九卷的定理20)提出了证明,大意如下:
对任何有限素数的集合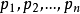 。在这里将会证明最少存在一个集合中没有的额外素数。令
。在这里将会证明最少存在一个集合中没有的额外素数。令 和
和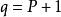 。那么q是素数或者不是,二者必居其一:
。那么q是素数或者不是,二者必居其一:
1、如果q是素数,那么至少有一个素数不在有限素数集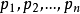 中。
中。
2、如果q不是素数,那么存在一个素数因子p整除q,如果p在我们的有限素数集中, p必然整除 P(既然 P是素数有限集中所有素数的积);但是,已知 p整除 ,如果 p同时整除P和q, p必然整除 P和q之差——
,如果 p同时整除P和q, p必然整除 P和q之差——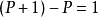 。但是没有素数能整除1,即有p整除q就不存在 p整除P。因此p不在有限集
。但是没有素数能整除1,即有p整除q就不存在 p整除P。因此p不在有限集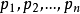 中。
中。
这证明了:对于任何一个有限素数集,总存在一个素数不在其中。所以素数一定是无限的。
很多时候有人会错误地指出欧几里得是用了反证法,他们假设证明起初考虑的是所有自然数的集合,或是集合内含有n个最小的素数,而不是任何任意的素数集合。欧几里得证明用的不是反证法,而是证明了一个有限集合中没有任何拥有特殊性质的元素。当中并没有反论的部分,但集合中的任何元素都不可以整除1。
文献中存在数个版本的欧几里得证明,包括以下的:
正整数n的阶乘n!可被2至 n的所有整数整除,这是由于它是这些数全部的乘积。因此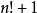 并不能被 2至 n(包括 n)的任何自然数所整除(所得的余数皆为1)。因此
并不能被 2至 n(包括 n)的任何自然数所整除(所得的余数皆为1)。因此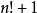 有两个可能性:是素数,或者能被大于 n所整除。在任一个案中,对所有正整数n而言都存在最小一个比n大的素数。所以结论就是共有无限个素数。
有两个可能性:是素数,或者能被大于 n所整除。在任一个案中,对所有正整数n而言都存在最小一个比n大的素数。所以结论就是共有无限个素数。
欧拉的证明另一个由瑞士数学家莱昂哈德·欧拉提出的证明,则使用了算术基本定理:每一个自然数都有一组独一无二的素因子排列。设P为所有自然数的集合,欧拉写下了:
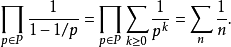 第一条等式是由乘积中每一项的等比数列公式所得。而第二个等式则是用于黎曼ζ函数的欧拉乘积。为了证实此点,可把乘积分配进和里面:
第一条等式是由乘积中每一项的等比数列公式所得。而第二个等式则是用于黎曼ζ函数的欧拉乘积。为了证实此点,可把乘积分配进和里面:
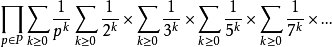
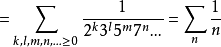
在这个结果中,每一个素数积都出现了正好一次,因此由算术基本定理可得这个和等于所有自然数的和。
右边的和是发散的调和级数。因此左边的和也是发散的。由于乘积内每一个项都是有限的,所以其项数必须为无限;因此得出共有无限个素数。
埃尔德什的证明埃尔德什·帕尔的第三种证明也是靠算术基本定理的。首先注意每一个自然数 都能被写成独一无二的
都能被写成独一无二的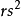 。其中
。其中 非平方数,或任何平方数的倍数(设
非平方数,或任何平方数的倍数(设 为能整除
为能整除 的最大平方数,并使
的最大平方数,并使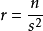 )。此时假设素数的数量为有限,且其数量为
)。此时假设素数的数量为有限,且其数量为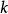 。由于每个素数只有一个非平方数的因子,所以根据算术基本定理,得出共有非平方数
。由于每个素数只有一个非平方数的因子,所以根据算术基本定理,得出共有非平方数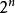 个。(见组合#在集合中取出k项元素及
个。(见组合#在集合中取出k项元素及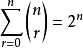 )
)
现在把一个正整数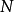 固定,并考虑1与
固定,并考虑1与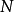 之间的自然数。 这些数每一个都能被写成
之间的自然数。 这些数每一个都能被写成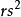 ,其中
,其中 为非平方数,
为非平方数,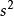 为平方数,例如:
为平方数,例如:
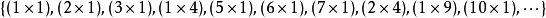
集合中共有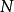 个不同的数。每一个都是由非方数和比
个不同的数。每一个都是由非方数和比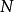 小的平方数组成。这样的平方数共有
小的平方数组成。这样的平方数共有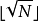 (见高斯符号的取底符号)。然后把这些小于
(见高斯符号的取底符号)。然后把这些小于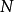 的平方数乘积与其余所有的非平方数相乘。这样得出的数一共有
的平方数乘积与其余所有的非平方数相乘。这样得出的数一共有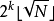 个,各不相同,因此它们包括了所有我们集合里的数,甚至更多。因此,
个,各不相同,因此它们包括了所有我们集合里的数,甚至更多。因此,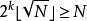 。
。
由于此不等式对足够大的 并不成立,因此必须存在无限个素数。
并不成立,因此必须存在无限个素数。
近期的证明皮纳西科胡安·帕布洛·皮纳西科(Juan Pablo Pinasco)写下了以下的证明。
设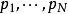 为最小的
为最小的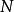 个素数。然后根据容斥原理可得,少于或等如
个素数。然后根据容斥原理可得,少于或等如 又同时能被那些素数中其中一个整除的正整数的个数为
又同时能被那些素数中其中一个整除的正整数的个数为
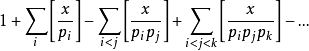
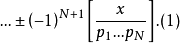
把全式除以 ,并且让
,并且让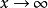 ,得
,得
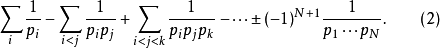 上式可被改写为
上式可被改写为
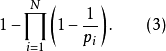 若除了
若除了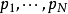 以外不存在其他素数的话,则式(1)与
以外不存在其他素数的话,则式(1)与 相等,而式(2)则等于
相等,而式(2)则等于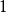 ,但很明显地式(3)并不等于1。因此除了
,但很明显地式(3)并不等于1。因此除了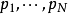 以外必须要存在其他素数。
以外必须要存在其他素数。
黄俊浩·彼得·黄(Junho Peter Whang)于2010年发表了使用反证法的证明。设{\displaystyle k}为任何正整数,{\displaystyle p}为素数。根据勒让德定理,则可得:

其中

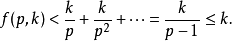
但若只存在有限个素数,则
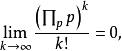 (上式分子呈单指数增长,但斯特灵公式指出分母的增长速度比分子快),这样就违反了每一个
(上式分子呈单指数增长,但斯特灵公式指出分母的增长速度比分子快),这样就违反了每一个 的分子要比分母大的这一点。
的分子要比分母大的这一点。
塞达克菲利浦·塞达克(Filip Saidak)给出了以下的证明,当中没有用到归谬法(而大部分欧几里得定理的证明都用了,包括欧几里得自己的证明),而同时不需要用到欧几里得引理,也就是若素数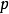 整除
整除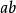 则也必能整除
则也必能整除 或
或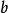 。证明如下:
。证明如下:
由于每个自然数(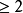 )最少拥有一个素因子,所以两个相邻数字
)最少拥有一个素因子,所以两个相邻数字 和
和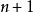 必定没有共同因子,而乘积
必定没有共同因子,而乘积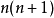 则比数字
则比数字 本身拥有更多因子。因此普洛尼克数的链:
本身拥有更多因子。因此普洛尼克数的链:
1×2 = 2 {2}, 2×3 = 6 {2, 3}, 6×7 = 42 {2,3, 7}, 42×43 = 1806 {2,3,7, 43}, 1806×1807 = 3263443 {2,3,7,43, 13,139}, · · ·
提供了一组素数集合无限增长的数列1。
使用π的无理性的证明以欧拉乘积来表示π的莱布尼茨公式可得
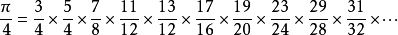
乘积的分子为奇数的素数,而每一个分母则是最接近分子的4的倍数。
若存在的素数是有限的话,上式所展示的就是π是一个有理数,而分母是所有与素数多1或少1的4的倍数的乘积,而这点违反了π实际上是无理数的这一点。
使用信息论的证明设只存在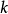 素数(
素数(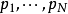 )。由算术基本定理可得,任何正整数
)。由算术基本定理可得,任何正整数 都能被写成:
都能被写成:
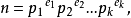
其中非负自然数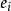 与素数的有限集合就足够重构任何数字。由于所有
与素数的有限集合就足够重构任何数字。由于所有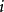 都遵守
都遵守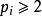 ,因此可得所有\
,因此可得所有\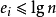 (其中{\displaystyle \lg }代表底数为2的对数)。
(其中{\displaystyle \lg }代表底数为2的对数)。
由此可得 的编码大小(使用大O符号):
的编码大小(使用大O符号):
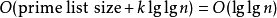 位元。
位元。
(其中prime list size为素数集合的大小)这编码比直接用二进制代表 要有效得多,二进制的话需要
要有效得多,二进制的话需要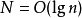 位元。无损数据压缩的一个已被确立的结果指出,一般不可能把
位元。无损数据压缩的一个已被确立的结果指出,一般不可能把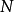 位元的信息压缩到少于
位元的信息压缩到少于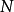 位元。由于
位元。由于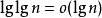 ,所以当
,所以当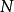 足够大时,以上的这个表示不成立。
足够大时,以上的这个表示不成立。
因此,素数的数量必不能为有限。
参阅狄利克雷定理
素数定理
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国