[科普中国]-穆尔-彭罗斯广义逆矩阵

穆尔-彭罗斯广义逆矩阵(Moore-Penrose generalized inverse matrix)是逆矩阵概念的推广，彭罗斯(R.Penrose)于1995年证明了对任一m×n阶矩阵A，都存在惟一的n×m阶矩阵X，它满足：1.AXA=A；2.XAX=X；3.(AX)*=AX；4.(XA)*=XA；则称X为A的穆尔-广义逆矩阵，简称M-P逆，记为A+。当A为n阶非异阵时，其逆A-1也满足条件1到4，故M-P逆确为通常逆矩阵的推广。在矛盾线性方程组Ax=b的最小二乘解中，x=A+b是范数最小的的一个解，任意矩阵的广义逆定义，最早是由穆尔(E.H.Moore)于1920年提出来的，根据实际问题的需要，一些学者还研究了其他各种类型的广义逆矩阵1。

基本介绍穆尔-彭罗斯广义逆矩阵是一种广义逆矩阵，设A是s×n复矩阵，如果n×s复矩阵G满足：

1.AGA=A；

2.GAG=G；

3.(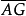 )′=AG；

4.(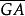 )′=GA，

则G称为A的穆尔-彭罗斯广义逆矩阵。显然，A与G互为穆尔-彭罗斯广义逆，任意的s×n复矩阵A有惟一的穆尔-彭罗斯广义逆，记为A+。

相关性质矩阵A的广义逆A+有如下的性质：

1.A+的秩r(A+)=r(A)=r(A′)；

2.(A+)+=A；

3.(A′)+=(A+)′，因此，若A是对称矩阵，则A+也是对称矩阵；

4.(A′A)+=A+(A+)′，因此，若A是半正定矩阵，则A+也是半正定矩阵；

5.AA+，A+A都是幂等矩阵。

穆尔-彭罗斯广义逆矩阵在最小二乘法中有用2。

相关说明设A为m×n的实矩阵，若n×m的矩阵H满足下列条件：

AHA= A，HAH=H，(AH)T=AH，(HA)T= HA (1)

则H称为A的穆尔-彭罗斯广义逆矩阵。该逆矩阵的唯一解通常表示为A+。可证明，若对A进行奇异值分解，即：

A= USVT， (2)

那么，根据正交矩陈的特性3：

A+= VS+UT， (3)

式中S+是n×m的矩阵，

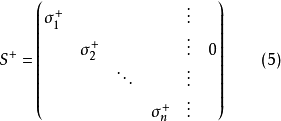其中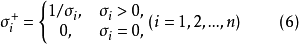

穆尔-彭罗斯广义逆是很多广义逆之一(Ben-Israel和Greville,1974)。也就是说，对当作逆的矩阵H有其它选择，因而对问题Ax= b可得不同的近似解。例如，在阻尼最小二乘方法(或脊式回归)中，矩阵H选为：

H= VFS+UT (7a)

该式中F是n×n对角滤波矩阵，其分量为：

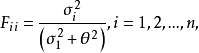(7b)

式中θ是大大小于最大奇异值σ1的调节参数。

该逆矩阵H的作用是产生估算值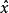,与穆尔-彭罗斯广义逆的解所得的值相比，可能它的沿相应于最小奇异值的奇异矢量分量被阻尼了。可以证明该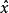是下列问题的解：

对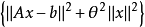求极小 (7c)

这样就代表了在数据拟合和解的大小限制之间的折衷。这种思路也用于非线性最小二乘法，即大家熟知的利文伯格-马今特法中(Levenberg-Marquardt method ) 。

与一般的逆矩阵不同，即使矩阵是奇异的，穆尔-彭罗斯的广义逆矩阵总是存在的。在构成这种广义逆矩阵时，必须小心地处理零奇异值。在式(6)中， 仅当σi>0时，定义σi+=1/σi；而当σi= 0时，则定义σi+=0。这就避免了一般求逆时由σi-1=1/σi带来的问题。而且，奇异值可帮助理解矩阵的秩和矩阵的条件。

通常矩阵秩定义为最大互不相关的列数，这样一个定义实际上很难应用于一般矩阵。然而若矩阵是三角形的，秩就是非零对角元素的数目。由于正交变换，比如在奇异值分解中的变换，并不影响秩，立即可以发现A的秩与其奇异值分解中S的秩相等，因此矩阵秩实用的定义是非零奇异值的数目。由于计算机精度有限，可能很难区别一个小奇异值和零奇异值，因而定义有效秩是大于某预定容限的奇异值数。容限反映了机器和数据的精度。

最后需指出，广义逆的奇异值分解(SVD)方法为我们的问题提供了有效的分析手段。哥鲁布和莱因思奇(Golub,Reinsch,1970)研究出奇异值分解的数值计算。在大多数计算中心，子程序库中一般都有奇异值分解子程序。虽然奇异值分解分析比乔勒基(Cholesky)法解正规方程要化去较多计算机时间， 但这是很值得的。按乘法运算的实际计数，奇异值分解需2mn2+4n3，而正规方程方法则需mn2/2 +n3/6。 例如，若解300个未知数的1000个方程，奇异值分解分析所需要的计算机时间约比正规方程方法长6倍。

但这里需指出正规方程方法的两大缺点。第一，正规方程矩阵的条件数是原始矩阵条件数的平方。这样，在组成正规方程和求解它时，需要把浮点精度t提高一倍才能避免计算中的舍人误差。第二，正规方程方法不能计算信息密度矩阵3。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学