在交换代数中,一个葛仑斯坦环(英文:Gorenstein ring)是对每个素理想的局部化皆为葛仑斯坦局部环的交换环。
介绍在交换代数中,一个葛仑斯坦局部环是一个内射维度有限的交换、局部诺特环。一个葛仑斯坦环(英文:Gorenstein ring)是对每个素理想的局部化皆为葛仑斯坦局部环的交换环。葛仑斯坦环是科恩-麦考利环的特例,它与凝聚对偶性定理(塞尔对偶性定理的推广)有密切关系。
葛仑斯坦环以数学家丹尼尔·葛仑斯坦命名。
其它定义对于局部环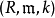 ,葛仑斯坦局部环的古典定义是:R是科恩-麦考利环,而且存在
,葛仑斯坦局部环的古典定义是:R是科恩-麦考利环,而且存在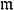 中的R-正则序列,使之生成一个不可约理想。在R为有限维诺特环时,下述性质等价:1
中的R-正则序列,使之生成一个不可约理想。在R为有限维诺特环时,下述性质等价:1
R的内射维度有限,记为n。
存在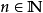 ,当
,当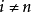 时,
时,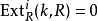 ,而且
,而且 。
。
存在 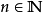 ,当i>n 时,
,当i>n 时,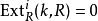 。
。
存在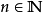 ,对某个i>n有
,对某个i>n有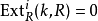 。
。
存在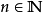 ,当i
,当i




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国