[科普中国]-艾伦伯格－斯廷罗德公理

在数学的代数拓扑学中，艾伦伯格－斯廷罗德公理（Eilenberg–Steenrod axioms）是拓扑空间的同调论的共有性质。符合这套公理的同调论的典型例子，是由塞缪尔·艾伦伯格和诺曼·斯廷罗德建立的奇异同调。

正式定义艾伦伯格－斯廷罗德公理用于从拓扑空间偶(X, A)范畴到阿贝尔群范畴的函子列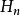，连同称为边界映射的自然变换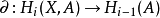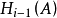（是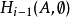的简记）。这套公理是：

1、恒同映射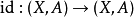在同调群中诱导的同态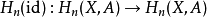是恒同同态。

2、设有空间偶的映射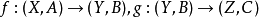，那么。

3、设有空间偶的映射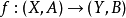，那么。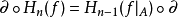

4、同伦：同伦的映射在同调群中诱导相同的同态。换言之，如果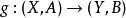同伦于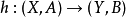，那么其诱导同态相同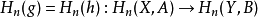：对所有的n>0。

5、切除：设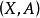是空间偶，U是X的子集，使得U的闭包包含在A的内部之中。那么包含映射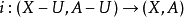在同调群中诱导的是同构。

6、维数：设P是单点空间，那么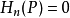对所有n≠ 0。

7、正合：任何空间偶(X,A)经由包含映射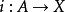和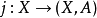，都在同调群中诱导出长正合序列：

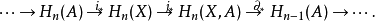约翰·米尔诺增加了一条公理：

可加性：设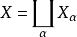是拓扑空间族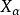的不交并，那么。

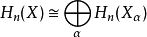设P是单点空间，那么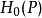称为系数群。12

结果同调群的一些结果可以用公理推导出，例如同伦等价空间的同调群是同构的。一些较为简单的空间的同调群可以直接从公理算出，比如n-球面。因此可以推导出(n-1)-球面不是n-球的收缩。用这个结果可以给出布劳威尔不动点定理的一个证明。3

维数公理如果一个同调论符合差不多所有艾伦伯格－斯廷罗德公理，但维数公理除外，便称为广义同调论（对偶概念为广义上同调论）。一些重要例子在1950年代发现，例如拓扑K-理论和配边理论，都是广义上同调论，并有与之对偶的同调论。4

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学