在数学特别是代数拓扑学中,霍普夫不变量(Hopf invariant)是球面之间某些映射的一个同伦不变量。1
历史1931年海因茨·霍普夫利用克利福德平行(Clifford parallel)构造了霍普夫映射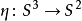 ,并通过利用圆周
,并通过利用圆周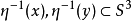 对任意
对任意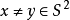 的环绕数(=1),证明了
的环绕数(=1),证明了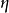 是本质的,即不同伦于常值映射。随后证明了同伦群
是本质的,即不同伦于常值映射。随后证明了同伦群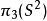 是由
是由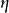 生成的无限循环群。1951年,让-皮埃尔·塞尔证明了对一个奇数维球面(n 奇)有理同伦群
生成的无限循环群。1951年,让-皮埃尔·塞尔证明了对一个奇数维球面(n 奇)有理同伦群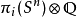 是零除非 i = 0 或 n。但对一个偶数维球面( n 偶),在
是零除非 i = 0 或 n。但对一个偶数维球面( n 偶),在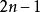 次处多出一个无限循环同伦。
次处多出一个无限循环同伦。
定义设 是一个连续映射(假设
是一个连续映射(假设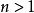 )。则我们可以构造胞腔复形
)。则我们可以构造胞腔复形
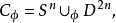 这里
这里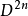 是2n-维圆盘通过
是2n-维圆盘通过 贴上一个
贴上一个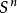 。 胞腔链群
。 胞腔链群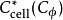 在度数n只是由n-胞腔自由生成,故它们在度数 0、n 与 2n是
在度数n只是由n-胞腔自由生成,故它们在度数 0、n 与 2n是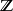 ,其余都是零。胞腔(上)同调是该链复形的(上)同调,因为所有边缘同态必然是零(注意到 n>1),上同调是
,其余都是零。胞腔(上)同调是该链复形的(上)同调,因为所有边缘同态必然是零(注意到 n>1),上同调是
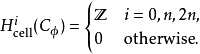 记这些上同调群的生成元为
记这些上同调群的生成元为
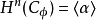 与
与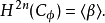
因为维数原因,这些类之间的所有杯积除了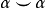 一定都是平凡的。从而作为一个环,上同调是
一定都是平凡的。从而作为一个环,上同调是
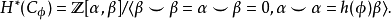 整数
整数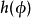 是映射
是映射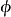 的霍普夫不变量。
的霍普夫不变量。
性质定理: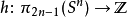 是一个同态。进一步,如果n是偶数,则h映到
是一个同态。进一步,如果n是偶数,则h映到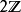 。2
。2
对霍普夫映射霍普夫不变量是1(这里 n=1,2,4,8,分别对应于实可除代数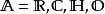 ,而二重复叠
,而二重复叠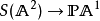 将球面上的一个方向送到它生成的子空间)。只有这些映射的霍普夫不变量是 1,这是最先由弗兰克·亚当斯(Frank Adams)证明的一个定理,后来迈克尔·阿蒂亚利用 K-理论重新给出了证明。3
将球面上的一个方向送到它生成的子空间)。只有这些映射的霍普夫不变量是 1,这是最先由弗兰克·亚当斯(Frank Adams)证明的一个定理,后来迈克尔·阿蒂亚利用 K-理论重新给出了证明。3
推广到稳定映射可以定义一种非常一般的霍普夫不变量概念,但需要一些同伦论知识预备:
设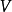 表示一个向量空间而
表示一个向量空间而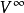 是其单点紧化,即对某个
是其单点紧化,即对某个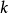 有
有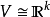 而
而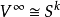 。如果
。如果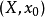 是任意带基点的空间(在上一节中不明确),如果我们去无穷远点为
是任意带基点的空间(在上一节中不明确),如果我们去无穷远点为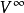 的基点,则我们可以构造楔积
的基点,则我们可以构造楔积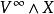 。
。
现在令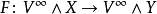 是一个稳定映射,即在约化垂纬函子下稳定。F 的(稳定)几何霍普夫不变量是
是一个稳定映射,即在约化垂纬函子下稳定。F 的(稳定)几何霍普夫不变量是
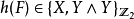 是从
是从 到
到 映射的稳定
映射的稳定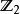 -等变同伦群中一个元素。这里稳定意为“在垂纬下稳定”,即通常等变同伦群在
-等变同伦群中一个元素。这里稳定意为“在垂纬下稳定”,即通常等变同伦群在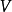 上(或
上(或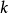 )的正向极限;而
)的正向极限;而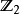 -的作用是
-的作用是 的平凡作用与交换
的平凡作用与交换 中两个因子。如果我们令
中两个因子。如果我们令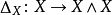 表示典范对焦映射而
表示典范对焦映射而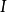 是是恒等,则霍普夫不变量由下式定义:
是是恒等,则霍普夫不变量由下式定义:
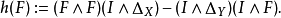 这个映射原本是从
这个映射原本是从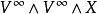 到
到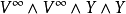 的映射。但在正向极限之下它成为映射的稳定同伦
的映射。但在正向极限之下它成为映射的稳定同伦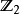 -等变群的典型元素。也有一个非稳定版本的霍普夫不变量
-等变群的典型元素。也有一个非稳定版本的霍普夫不变量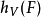 ,为此我们必须考虑向量空间 V。
,为此我们必须考虑向量空间 V。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国