一元n次方程(equation of degree n with one unknown)是一元n次多项式所确定的方程,指方程a0xn+a1xn-1+…+an=0 (a0≠0),当n≥3时,称为高次方程.研究一元n次方程的根,包括根的存在、根式解、根的界和根的个数等,曾经是代数学的中心问题,一元n次方程的系数和有理常数以及对这些数进行加、减、乘、除和开整数次方的符号组成的式子,称为方程的根式,根式解就是求将代数方程的根用方程系数的根式表达出来,n次方程的根式解,亦称为代数解法,三次方程与四次方程的根式解于16世纪由意大利数学家给出,此后自然地开始寻求五次以及五次以上代数方程的根式解,这种尝试一直继续近三个世纪,经过莱布尼茨(G.W.Leibniz)、范德蒙德(A.-T.Vandermonde)、拉格朗日(J.-L.Lagrange)、鲁菲尼(P.Ruffini,)等人的艰辛努力,直到19世纪才由阿贝尔(N.H.Abel,)解决,他证明了一般的n (n≥5)次方程不能用根式解,不久伽罗瓦(E.Galois,)用群论方法得出了方程可用根式解的充分必要条件1。
基本介绍如果f(x)是一元n次多项式,那么f(x)=0叫做一元n次方程,一元n次方程的一般形式是:
f(x)=anxⁿ+an-1xⁿ-1+…+a1x+a0=0 (其中an≠0,n∈N.)……①
当n>2时,称为一元高次方程。
(1)若ai(i=0,1,2,…,n)是复数,则称方程为复系数一元n次方程,n>2时为复系数高次方程。
(2)若ai(i=0,1,2…,n)是实数(或有理数、整数),则称方程①为实系数(或有理系数、整系数)一元n次方程.n>2时,也称实系数(或有理系数、整系数)高次方程.。
(3)如果有α,使得f(α) =0,则α是方程f(x)=0的根2。
一元n次多项式的解一元一次方程、一元二次方程、一元三次方程分别有一个根、二个根、三个根,它们都可以用代数解法来解,并且有求根公式。可以证明一元四饮方程有四个根,并且可以用代数解法求解。 当n > 4时,根据伽罗华理论, 一般形式的n次方程不能用代数解法来解3。
关于一元n次方程的根的个数,我们有以下定理和推论。
定理1 (代数基本定理)一元n次方程至少有一个根。
如果f (x )的次数大手1, 那么根据定理1可以知道,方程f (x) =0至少有一个根,设这个根是α,那么由于f(α) =0,根据因式定理可以知道, f(x)=(x-α)q(x).,因为x-α和q (x)的次数都低于f(x)的次数,所以f(x)可约,由此我们得到:
推论1 任何次数大于1的多项式都是可约的3。
推论2 f(x)=a0xⁿ+a1xⁿ-1+…+an-1x+an=0 (其中a0≠0,n∈N)的标准分解式是
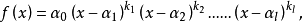 式中
式中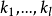 都是正整数,
都是正整数,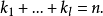
根据f (x)的标准分解式可以知道,如果x=αi(i=1,2,...,),那么f(αi) =0,所以αi是方程f(x)=0的根。这就是说,f(x)的毎一个一次因式的根都是方程f(x)=0的根,如果x-αi是f (x)的k重因式,那么就说αi是方程f(x)=0的k重根,在讨论根的个数吋,k重根当作k个计算。
例如,方程(x-2)3(x+1)2(x-1)=0有三重根2,二重根-1,単根1,因此,这个方程一共有6个根。
定理2一元n次方程有n个根并且只有n个根。
证根据定理1的推论2,任何一个一元n次方程f(x)=0,如果把f(x)分解成标准分解式,就得
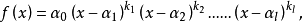 式中
式中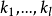 都是正整数,
都是正整数,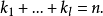
因为方程有k1重根α2,k2重根α2,..., kl重根αl,共 有k1+k2+...+kl=n个根,又因为f (x)的标准分解式是唯一的,所以f(x)=0有n个根并且只有n个根。
下面是一元n次方程的根和系数的关系的定理。
定理3 (韦达定理)如果一元n次方程f(x)=a0xⁿ+a1xⁿ-1+…+an-1x+an=0 (其中a0≠0,n∈N)的根是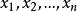 ,那么
,那么
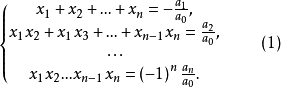
韦达定理的逆定理也成立,也就是说,如果n个数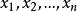 满足关系式(1),那么
满足关系式(1),那么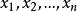 必为方程f(x)=a0xⁿ+a1xⁿ-1+…+an-1x+an=0 (其中a0≠0,n∈N)的n个根3。
必为方程f(x)=a0xⁿ+a1xⁿ-1+…+an-1x+an=0 (其中a0≠0,n∈N)的n个根3。
一元一次方程ax+b=0(a≠0)的解为
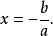
韦达(Viete)给出了一元二次方程ax2 +bx+c=0(a≠0)的一个求根公式为
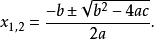
一元三次方程有三个根,有可能都是实数根,也有可能是一个实数根和两个互为共轭的复数根,不过,16世纪的数学家还没有虚数的概念4。
一元四次方程由费拉里(Ferrari)解决,方法是将一元四次方程化为两个一元二次方程与一个一元三次方程求解。
拉格朗日发现不能用求一元二次方程、一元三次方程、一元四次方程的方法来求解一元五次和一元五次以上的代数方程。
鲁菲尼(Ruffini)-阿贝尔(Abel)定理:一般地,五次和五次以上的代数方程是不可能由代数根式求解。
伽罗瓦(Galois)建立了一般的理论:五次和五次以上方程代数可解的判别准则,伽罗瓦为群论奠定了基础,群论在物理学中被用来研究对称性4。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国