[科普中国]-低密度同位元检查累积码

低密度同位元检查累积码由低密度奇偶检查码（low-density parity-check，LDPC)和一个累加器组成。其运作方式为Bit Node以二位元模组的方式相加到Check Nodes，根据tanner graph。 然后，Check nodes的值以modulo-two被累加。 利用这种方式，通道解码端的解码器可以避免有一个check node没有被连结到任何bit node的状况。 经过累加后，累加的位元会被存在一个缓冲器中，再逐渐传送到解码器。

简介低密度同位元检查累积码是一种信道编码方法，低密度同位元检查累积码有三个阶段。第一个阶段是一个可逆线性转换矩阵，其中有资料来源序列。 第二个阶段是一个一个rate的累加器，可以转换长度为L的序列。第三个阶段是变更或置换这个序列。 这个序列接下来会传送到解码器，总共需要传送的码数量由解码器的回馈决定。低密度同位元检查累积码可以应用在许多编解码应用的系统当中。

低密度奇偶检查码低密度奇偶检查码（Low-density parity-check code，LDPC code），是线性分组码（linear block code）的一种，用于更正传输过程中发生错误的编码方式。在1962年，低密度奇偶检查码(LDPC code)即被Gallager提出，并被证明其错误校正能力非常接近理论最大值，香农极限(Shannon Limit)；不过受限于当时技术，低密度奇偶检查码并无法实现。低密度奇偶检查码被重新发现，并随着集成电路的技术演进，低密度奇偶检查码的实现逐渐可行，而成为各种先进通信系统的频道编码标准。

低密度奇偶检查码是基于具有稀疏矩阵性质的奇偶检验矩阵建构而成。对(n, k)的低密度奇偶检查码而言，每k比特数据会使用n比特的码字(codeword)编码。以下是一个被(16, 8)的低密度奇偶检查码使用的奇偶检验矩阵H。当中可以见得矩阵内的元素1数量远少于元素0数量，所以具有稀疏矩阵性质，也就是低密度的由来。

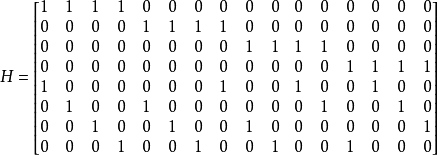
低密度奇偶检查码的解码，可对应成二分图(bipartite graph)作表示。下方的二分图是依照上述奇偶检验矩阵H建置，其中H的行(column)对应至check node，而H的列(row)对应至bit node。check node和bit node之间的连接，由H内的元素1决定；好比H中第一行(column)和第一列(row)的元素1，使check node和bit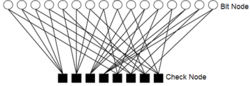node两者各自最左手边的第一个彼此连接。

低密度奇偶检查码的解码算法，主要基于有迭代性(iterative)的置信传播(belief propagation)；整个解码流程如下方所示：

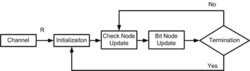
当接收数据R从通信频道(channel)进入低密度奇偶检查码的解码器，解码器会对消息作初始化(initialization)。

check node根据互相连接的多个bit node内的数据做更新运算(update)。

bit node对相连接的多个check node内的数据做更新运算。

观察终止(termination)条件，来决定是否继续迭代计算。

累加器在中央处理器中，累加器 (accumulator) 是一种寄存器，用来储存计算产生的中间结果（在运算器中，形成和存放运算 结果的寄存器）1；或指可以存储一数并接受另一数，将两者相 加后存储其总和的设备称累加器。累加器还 具有移位、读出信号、清除、求补等功能。

如果没有像累加器这样的寄存器，那么在每次计算 (加法，乘法，移位等等) 后就必须要把结果写回到 内存，也许马上就得读回来。然而存取主存的速度是比从算术逻辑单元到有直接路径的累加器存取更慢。标准的例子就是把一列的数字加起来。一开始累加器设定为零，每个数字依序地被加到累加器中，当所有的数字都被加入后，结果才写回到主存中。

信道编码一种为了提高通信系统可靠性而对传输信号进行的编码。即使所传输信号内部具有更强的规律性和相关性，以使信号受干扰而损伤时仍能正确恢复原有信息的处理过程。即为了适应信道条件(如频带宽度限制、波段、功率、通信时间等)和满足通信的要求(如可靠性、有效性等)，需要对所传输的信号进行的某种变换。信道编码的理论基础是信息论中的信道编码定理，它从理论上解决理想编码器的存在性问题。信道编码的具体方法属于差错控制技术。

能检出和纠正传输中产生错误的编码。用于检错的码叫检错码；用于检错与纠错相结合的码称为“纠错码”。按纠错类型可分纠随机错误码、纠突发错误码，纠字节(byte)错误码和纠运算错误的算术运算码等。按构造可分分组码和树码。分组码是将M个符号序列分别映射成长度为n的码字。如该映射规律满足线性关系，则称为“线性码”，否则称为“非线性码”。树码具有树形结构，可用树形图描述。状态有限的树图可简并成格状图，称为格状码。由分组码和树码级连的码称为“级连码”，它具有更强的纠错性能并更易于实现。纠错码的纠错能力和有效的译码算法是研究信道编码的焦点。Turbo码和低密度奇偶校验(LDPC)码是两种性能逼近仙农限的最令人瞩目的纠错码。信道编码已在各类数字通信系统中得到广泛应用。其发展趋势是调制与纠错相结合，信道编码与信源编码相结合等。

本词条内容贡献者为:

王慧维 - 副研究员 - 西南大学