[科普中国]-玻尔兹曼因子

在物理学中，玻尔兹曼因子是一个权重因子，它决定了在温度T时处于热力学平衡的多状态系统中状态i的相对概率。

简介在物理学中，玻尔兹曼因子是一个权重因子，它决定了在温度T时处于热力学平衡的多状态系统中状态i的相对概率：

其中是玻尔兹曼常数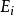，是状态的能量。两个状态的概率之比，由它们的玻尔兹曼因子的比给出。

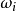玻尔兹曼因子本身并不是一个概率，因为它还没有归一化。为了把玻尔兹曼因子归一化，使其成为一个概率，我们把它乘上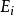能级的对应的量子态数，再除以系统所有可能的状态的玻尔兹曼因子之和Z（配分函数）。这便给出了玻尔兹曼分布。

从玻尔兹曼因子可以推导出麦克斯韦-玻尔兹曼统计、玻色-爱因斯坦统计和费米-狄拉克统计，它们分别描述了经典粒子、玻色子和费米子的统计规律。1

麦克斯韦-玻尔兹曼统计麦克斯韦—玻尔兹曼统计是描述独立定域粒子体系分布状况的统计规律。所谓独立定域粒子体系指的是这样一个体系：粒子间相互没有任何作用，互不影响，并且各个不同的粒子之间都是可以互相区别的，在量子力学背景下只有定域分布粒子体系中的粒子是可以相互区分的，因此这种体系被称为独立定域粒子体系。而在经典力学背景下，任何一个粒子的运动都是严格符合力学规律的，有着可确定的运动轨迹可以相互区分，因此所有经典粒子体系都是定域粒子体系，在近独立假设下，都符合麦克斯韦-玻尔兹曼统计。1

参见玻尔兹曼关系（等离子体物理学）

玻色–爱因斯坦统计

费米-狄拉克统计

蒙地卡罗方法

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学