[科普中国]-德古阿定理

德古阿定理是勾股定理的三维形式，以法国数学家让·保罗·德古阿·德马尔弗（Jean Paul de Gua de Malves）命名1。

定义若从一个正六面体截下一角O形成一截角锥（记为ABCO），则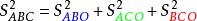

勾股定理勾股定理又称商高定理、毕达哥拉斯定理、毕氏定理、百牛定理，是平面几何中一个基本而重要的定理。勾股定理说明，平面上的直角三角形的两条直角边的长度（古称勾长、股长）的平方和等于斜边长（古称弦长）的平方。反之，若平面上三角形中两边长的平方和等于第三边边长的平方，则它是直角三角形（直角所对的边是第三边）。

勾股定理是人类早期发现并证明的重要数学定理之一。

据《周髀算经》中记述，公元前一千多年周公与商高论数的对话中，商高就以三四五3个特定数为例详细解释了勾股定理要素，其一，“以为句广三，股修四，径隅五”。其二，“既方其外，半之一矩，环而共盘，得成三四五。两矩共长二十有五，是谓积矩。”首先肯定一个底宽为三，高为四的直角三角形，弦长必定是五。最重要的是紧接着论证了弦长平方必定是两直角边的平方和，确立了直角三角形两条直角边的平方和等于斜边平方的判定原则。其判定方法后世不明其法而被忽略。

此外，《周髀算经》中明确记载了周公后人陈子叙述的勾股定理公式：“若求邪至日者，以日下为勾，日高为股，勾股各自乘，并而开方除之，得邪至日”。

赵爽在《周髀算经注》中将勾股定理表述为“勾股各自乘，并之，为弦实。开方除之，即弦2”。

古埃及在公元前2600年的纸莎草就有（3,4,5）这一组勾股数，而古巴比伦泥板涉及的最大的一个勾股数组是（12709，13500，18541）。

有些参考资料提到法国和比利时将勾股定理称为驴桥定理，但驴桥定理就是等边对等角，是指等腰三角形的二底角相等，非勾股定理。

即在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么可以用数学语言表达：

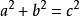
余弦定理是勾股定理的一个推广。勾股定理现约有400种证明方法，是数学定理中证明方法最多的定理之一。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学