[科普中国]-精确数

精确数(exact number)亦称精确值，是数学的基本概念之一，一个数若能准确地表示某一个量，则这个数就称为该量的精确数，例如4本书的4，6张桌子的6都是精确数1。

基本介绍用来表示量的准确值的数叫做准确数。

在计算中，我们遇到的数值通常有两种：一种是完全精确的数(真值)，称为精确数或准确数；一种是近似数(近似值)，，它是与精确数非常接近、相差很小的数。如用1.41、1.4142代替无理数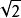，这里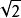是精确数(真值)，而1.41、1.4142都是近似值。

精确数是指没有误差的数。如某正方形的边长为a，则其周长为4a。其中的4即是精确数，它没有误差。常用整数或分数表示精确数，但精确数也可使用小数或无理数表示。如1mm=0.001m，此处的0.001即是精确数。直径为D的圆的周长为πD，边长为a的正方形的对角线长度为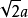。此处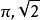，也是精确数。但在计算中，无理数常使用有限精度的小数参与运算，这时，参与运算的无理数就成了近似数。含有误差的数值，统称为近似数。近似数的精度，使用有效数字描述2。

相关概念近似值：近似于准确值的值称为近似值。较准确值小的近似值称为不足近似值，较准确值大的近似值称为过剩近似值3。

近似数：用来表示量的近似值的数叫做近似数。

误差：近似数与它的准确数之差称为误差。误差按其来源可分为测量误差、截断误差和舍人误差。

绝对误差：一个近似数与它的准确数的差的绝对值叫做这个近似数的绝对误差。用a表示近似数，A表示它的精确数，那么近似数a的绝对误差就是|a－A|。

相对误差：一个近似数的绝对误差对于它的准确数所占的百分数，叫做这个近似数的相对误差。用a表示近似数，A表示它的精确数，那么近似数a的相对误差就是

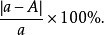
相对误差能确切地表示近似值的近似程度。在不知道准确数的情况下，我们就用绝对误差对近似数所占的百分数作为这个近似数a的相对误差。

截断误差：在一般计算问题中，为了便于计算，将复杂的表达式用一近似表达式来代替，而称正确表达式与近似表达式之差为截断误差。例如，用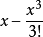代替sinx时，截断误差为

舍入误差:在计算过程中出现的位数较多的数，往往为了计算方便或是受到计算工具的限制，要用位数较少的数来代替。代替的方式通常采用四舍五入、只舍不人等规则。由此产生的误差称为舍入误差。

例如，用3.14代替3.14159265 ...时，舍人误差为0.00159265...。

四舍五人法：一种近似数的截取法。其方法是把要处理的数保留到某一指定的数位为止，后面的数字全部舍去， 如果舍去的第一位数字是5或者大于5，在保留的最后一位数字上加1；如果舍去的第一位数字小于5，保留的数就不变。

去尾法：一种近似数的截取法。其方法是，把要处理的数保留到某一指定的数位为止，后面的数字全部舍去。

例如，3. 14159...用去尾法截取到千分位(即精确到0.001 )就得近似数3.141。

进一法：一种近似数的截取法。其方法是，把要处理的数保留到某一指定的数位为止，后面的数字全部舍去，但是如果舍去的数字不都是零，那么保留的最后一位数字上加1。

例如，5. 43106用进一法截取到千分位，就得近似数5.432

抹尾凑整法：一种近似数的截取法。抹尾凑整规则是:要把一个数抹尾凑整到n位有效数字，就须先把这个数的第n位右边的全部数字都抹去，(1)如果被抹去的部分大于第n位数字的半个单位，则在第n位数字上加1; (2)如果小于第n位数字的半个单位，则保持第n位数字不变；(3)如果恰好是第n位数字的半个单位，则当第n位数字为奇数时就加1；为偶数时就不变。当某一个数按此规则抹尾凑整时，我们就说它精确到n位有效数字。

例如，将1.34996抹尾凑整到5位有效数字为1.3500；4位有效数字为1.350；3位有效数字为1.35；2位有效数字为1.3(1.34996中4996小于1/10位的半个单位)。

上述抹尾凑整的方法可归结为“四舍六入，五凑偶”，这种规则比旧的四舍五人规则误差小。

有效数字：一个近似数的绝对误差，如果不大于它最末一位的半个单位，那么这个近似数从左边第一个不是0的数字起，到末位数字为止，所有的数字都叫做这个近似数的有效数字。

例如，0.009995的近似值0.01000有四个有效数字1、0、0、0。

用四舍五人法截取得到的近似数，从第一个不是0的数字起到保留的数位为止，所有的数字都是有效数字。

例如，0.0016有两个有效数字1，6；1.60有三个有效数字1，6，0；1.6有两个有效数字1，6。这里1.60比1.6的精确度高。

如果一个近似数是整数，而且末尾带有几个0，则必须指明这个近似数精确到哪一位，才能确定它有几个有效数字。

例如，15000精确到百位，它有3个有效数字1，5，0；一般地用15000 (±50)或者1.50x104来表示。

准确度和精确度：准确度一由有效数字的个数来确定；精确度——由末一位有效数字的单位来确定。如101.7就说它准确到四位有效数字；它的末一位有效数字是小数点后1位，就说它精确到小数后1位。又如，1.234，12. 34，123.4三个数都准确到四位有效数字，但它们的精确度不同，第1个数最精确; 而三个数1.234，0.234，0.034的精确度虽然相同，都精确到小数点后第3位，但准确度不同，第1个数最准确。

在进行近似数的加减时，我们应考虑精确度；在进行近似数的乘除运算时，决定结果的可靠程度是准确度(有效数字)。所以二者在近似计算中要结合起来运用。

科学计数法：是一种科学技术上常用的记数法。它是把一个正数记成ax10n的形式，其中1≤a