[科普中国]-完全一元二次方程

完全一元二次方程是一类简单的代数方程，即具有标准形式且一次项系数与常数项均不为零的一元二次方程。当一次项系数与常数项至少有一个为零时则称为不完全一元二次方程。

简介完全一元二次方程是一类简单的代数方程，即具有标准形式且一次项系数与常数项均不为零的一元二次方程。

例如x2-2x+1=0。当一次项系数与常数项至少有一个为零时则称为不完全一元二次方程。1

一元二次方程只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。标准形式为：ax²+bx+c=0（a≠0）。

一元二次方程必须同时满足三个条件：

①是整式方程，即等号两边都是整式，方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。

②只含有一个未知数；

③未知数项的最高次数是2。

求解方法直接开平方法形如(nx+m)²=p(p≥0)的一元二次方程可采用直接开平方法解完全一元二次方程。

注意：

①等号左边是一个数的平方的形式而等号右边是一个常数。
②降次的实质是由一个一元二次方程转化为两个完全一元一次方程。
③方法是根据平方根的意义开平方。

配方法将方程配成(x+m)²=n的形式，再利用直接开平方法求解的方法。

用配方法解方程的步骤：

①把原方程化为一般形式；

②方程两边同除以二次项系数，使二次项系数为1，并把常数项移到方程右边；

③方程两边同时加上一次项系数一半的平方；

④把左边配成一个完全平方式，右边化为一个常数；

⑤进一步通过直接开平方法求出方程的解，如果右边是非负数，则方程有两个实根；如果右边是一个负数，则方程有一对共轭虚根。

求根公式法用求根公式法解一元二次方程的一般步骤为：

①确定方程a，b，c的值（注意符号）；

②求出判别式的值，判断根的情况；

③在判别式≥0的前提下，把a、b、c的值代入公式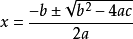进行计算，求出方程的根。

因式分解法因式分解法即利用因式分解求出方程的解的方法。

因式分解法解一元二次方程的一般步骤：

①移项，使方程的右边化为零；

②将方程的左边转化为两个一元一次方程的乘积；

③令每个因式分别为零

④括号中x，它们的解就都是原方程的解。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所