无理方程组(system of irrational equations)是一种常用的代数方程组。即至少有一个是无理方程的代数方程组,其解法的一般步骤是:1.化无理方程为有理方程。2.解由有理方程组成的方程组。3.验根1。
基本介绍解无理方程组的基本思想方法是把它转化为有理方程组来解,解无理方程组时,由于方程的变形可能会产生增根,因此解无理方程组必须验根。
解无理方程组时,可以利用解无理方程的一些基本方法,将方程组化为有理方程组来求解。不论采用什么方法,其目的都是要化繁为简,减少方程中未知数的个数,或降低未知数的次数。必须注意,当无理方程转化成有理方程求得解后,要及时进行检验,舍去不合题意的根,以减少不必要的运算与错误2。
例题解析【例1】解下列方程组:
①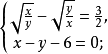
②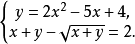
③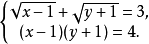
解:①
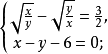
设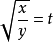 ,则方程
,则方程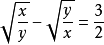 可化为
可化为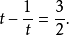
整理得
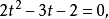 解得
解得
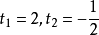 其中
其中 不合题意舍去。所以
不合题意舍去。所以
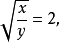 即
即
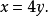 解方程组
解方程组
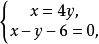 得
得
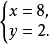 经检验,原方程组的解为
经检验,原方程组的解为
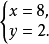 ②
②
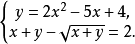
设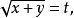 则方程
则方程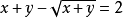 可化为
可化为
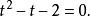 解得
解得
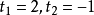 其中
其中 不合题意舍去,所以
不合题意舍去,所以
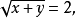 即
即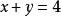 。
。
解方程组
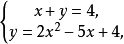 得
得
 经检验,原方程组的解为
经检验,原方程组的解为

③
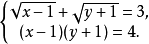
设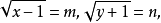 则原方程组可化为
则原方程组可化为
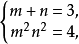 即
即
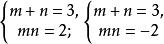 其中
其中
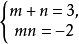 不合题意舍去。解方程组
不合题意舍去。解方程组
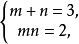 得
得
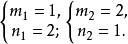 所以
所以
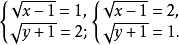 解得
解得
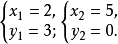
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国