分式方程组(system of fractional equations)是一种常用的代数方程组,在有理方程组成的方程组中,至少有一个方程是分式方程时,称为分式方程组。解分式方程组时,常把方程组中各个分式方程的两边乘以适当的整式(分母的最低公倍式),将它变形为整式方程,然后解这个整式方程组,由于对方程两边乘以适当的整式非同解变形,有增根的可能,因此,必须把求得的整式方程组的解代入所乘的整式或代入原方程组进行检验1。
基本介绍方程组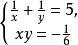 中,方程的分母中含有未知数,像这样的方程组称为分式方程组。
中,方程的分母中含有未知数,像这样的方程组称为分式方程组。
解分式方程的基本思想为“化分式方程为整式方程”,同样,解分式方程组的基本思想为“化分式方程组为整式方程组”,也就是把方程组中的每一个分式方程都转化为整式方程。
解分式方程组可以把它化成整式方程组后再求解,有些时候也可以根据方程组的特点用不同的方法解题。
解分式方程组时,由于变形过程中,曾用含未知数的整式去乘方程的两边,并约去分母,因此可能产生增根,所以验根这个步骤对解分式方程组来说,也是必不可少的2。
例题解析【例1】解方程组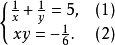
解:因为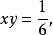 所以
所以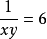 ,原方程组可化为
,原方程组可化为
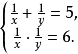 设
设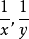 是一元二次方程
是一元二次方程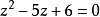 的两个解,解得
的两个解,解得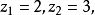 即
即
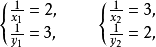 所以
所以
 经检验
经检验 都是原方程组的解。
都是原方程组的解。
【例2】解方程
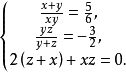
分析 此题若用去分母法,变形为三元二次方程组,计算较繁,如果能转化为它的倒数来处理,问题就化难为易了。
解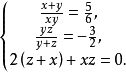 取倒数
取倒数
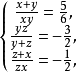 拆项得
拆项得
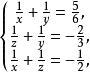 三个方程相加整理得:
三个方程相加整理得:
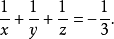 再用这个方程减上面每个方程可求x,y,z,解得
再用这个方程减上面每个方程可求x,y,z,解得
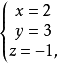 经检验知是原方程组解2。
经检验知是原方程组解2。
故原方程的解为
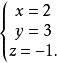
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国