[科普中国]-同解变形

同解变形（equivalent transformation）是解方程(组)所涉及的一个概念，用一个方程(组)的同解方程(组)代替这个方程(组)，这种代换称为原方程(组)的同解变形。通常，在解方程(组)的过程中，主要是不断进行同解变形；如果出现了非同解变形，则应对得出的结果进行讨论或验根，找出遗解舍弃增解，关于不等式(组)的同解变形，意义和方程同解变形类似。

基本介绍对于一个方程，进行某种变形后，得到与原方程同解的一个新的方程，这种变形叫做同解变形。

通常，在解方程的过程中，主要是不断进行同解变形；如果出现了非同解变形，则应对得出的结果补充讨论或验根。关于方程组、不等式、不等式组，同解变形的意义和上述相仿。

对于一个方程(或不等式)，指出在保持同解性前提下，所允许进行的一些变形，这些结论统称同解定理。

方程的同解变形使方程变为它的同解方程的过程叫做同解变形。关于方程的同解变形，主要有下面的三个定理1。

定理1在方程的两边都加上同一个整式(单独的一个数也是整式)，所得方程与原方程同解。

用此定理时一定要注意加上的解析式是整式的条件，否则所得方程不一定与原方程同解。例如，方程2x-1=3的两边都加上分式4/(x-2)所得方程2x-1+4/(x-2)=3+4/(x-2)与原方程并不同解。因为原方程的解x=2使新方程的分母为零，方程无意义。

由定理1易得到移项法则：方程中的项改变符号后可以从方程的一边移至另一边。

定理2方程的两边都乘以同一个对方程的未知数的一切允许值都有意义且值不为零的解析式，所得方程与原方程同解。

显然，方程两边都乘以同一个非零的数也符合定理条件。

用此定理时，必须注意所乘解析式对原方程中未知数的一切允许值都有意义且值不为零的两个条件.例如，把方程x²-4=3x的两边都乘以解析式1/(x-4)所得方程(x²-4)/(x-4)=3x/(x-4)与原方程并不同解，原因是所乘解析式并不是对原方程未知数的所有允许值都有意义.当x=4时，1/(x-4)无意义，而x=4是原方程的一个解.又如，方程(x²+1)(2x-3)=(x²+1)(x-1)可以认为是由方程2x-3=x-1的两边都乘以解析式x²+1所得.这两个方程在实数集里同解，在复数集内不同解.原因是在实数集内x²+1≠0，在复数集里x²+1的值有为零的时候，使x²+1=0的x值是方程(x²+1)(2x-3)=(x²+1)(x-1)的解而不是原方程2x-3=x-1的解，这就产生了增根。

定理3若方程的一端为零，另一端是几个因式的乘积，则使各个因式分别等于零而得到的几个方程与原方程同解。

本定理是用因式分解的方法解方程的理论依据。

例如，要解方程x³-3x²-x+3=0，可将方程左端分解因式，得到方程

(x+1)(x-1)(x-3)=0

据定理3，只要解下面三个方程

x+1=0，x-1=0，x-3=0

得到原方程的解为：

x1=-1，x2=1，x3=3.

在解方程时，若进行的变形都符合上面的三条定理，则保证是同解变形，所得方程之解皆为原方程之解，且不会失根，故不必进行检验1。

方程组的同解变形方程组的同解定理有：

1.方程组里的任一方程用它的一个同解方程去代替，所得的方程组和原方程组同解。

2.方程组里的某一方程如是其中一个未知数用另一些未知数来表示的等式。那么，在这方程组里的另一些方程中，凡出现该未知数时都用这个表达式去代替，所得的方程组和原方程组同解。

3.方程组里的一些方程的两边分别相加(减)，所得到的方程去代替参加运算的任一方程，所得的方程组和原方程组同解。

4.方程组里的某一方程如是一边为若干个因式的乘积，另一边为零的形式，令这些因式分别为零而得到若干个方程，将这些方程逐一和原方程组中的其余方程组成新的方程组，那么原方程组的解即是这些新的方程组的解的全体2。

不等式的同解变形不等式的同解定理有：

1.不等式f(x)>g(x)和不等式g(x)g(x)和不等式f(x)+h(x)>g(x)+h(x)同解。

3.如果h (x)对未知数的一切可能值恒取正值，则不等式f(x)>g(x)和f(x)·h(x)>g(x)·h(x)同解;不等式f(x)>g(x)和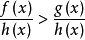同解。

4.如果h(x)对未知数的一切可能值恒取负值，则不等式f(x)>g(x)和f(x)·h(x)g(x)和同解2。

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司