[科普中国]-不等量公理

不等量公理(axioms of inequality)是数学的基本公理之一，它是解不等式的依据，在初等数学中，常把下列各公理统称为不等量公理：1.全量大于它的任一部分；2.不等量加(减)等量，其和(差)不等，原来大的仍大；3.等量减不等量，其差不等，减去大的反而较小；4.不等量加不等量，两个大量的和大于两个小量的和；5.第一量大于第二量，第二量大于第三量，则第一量大于第三量。其中，有些公理(例如第1条)最早出自欧几里得(Euclid)的《原本》1。

基本介绍不等量公理常指以下公理：

(1)不等量加上或者减去等量，原来大的仍大；

(2)不等量乘以或者除以同一个正数，原来大的仍大；

(3)不等量加不等量，大量的和大于小量的和；

(4)等量减不等量，减去大的，差反而小；

(5)第一量大于第二量，第二量大于第三量，则第一量大于第三量；

(6)全量大于它的任何一部分；

(7)在不等式中，一个量可以用它的等量来代替。

在研究不等关系时，常要用到一些关于不等量的公理。其中有些我们在学习代数时已经在应用，如：不等量加上或者减去等量，原来大的仍旧大；不等量乘以或者除以同一个正数，原来大的仍旧大；在不等式中，一个量可以用它的等量来代替。此外，还常用到下面一些不等量的公理：

(1)第一量大于第二量，第二量大于第三量，第一量就大于第三量。例如，∠1>∠2，∠2>∠3，那么∠1>∠3。

(2)不等量加不等量，大量的和大于小量的和。例如∠1>∠2，∠3>∠4，那么∠1+∠3>∠2+∠4。

(3)全量大于它的任一部分量。例如，C是线段AB上一点，那么AB>AC。

例题解析**【例1】** 证明：从直线外一点到这条直线上各点所联的线段中，和这条直线垂直的线段最短。

已知：PO⊥AB，O为垂足，E为AB上异于O的一点，

求证: PE> PO。

证明：延长PO至Q，使PO= OQ，

以AB为轴翻转P点所在的半平面(图1)。

∵PO⊥AB，(已知)，

∴翻转后射线OP与OQ重合，

又OP= OQ，

∴P、Q重合，

则 PE= EQ，

PE+EQ= 2PE，

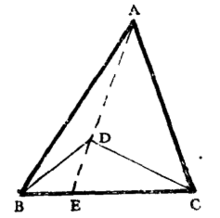
但PQ∠BAE，∠EDC>∠EAC，相加得∠BDC>∠BAC2。

本词条内容贡献者为:

武伟 - 高级工程师 - 天津直升机有限责任公司