[科普中国]-一元方程

一元方程(monadic equation)是一种最简单的方程，指含有一个未知数的方程，更确切的意义是：如果一个方程中，有若干个字母，当把其中某一个字母当成未知数，而把其余字母当成已知数时，方程就称为该字母的一元方程。在讨论多元方程时，也可以出现除一个元外，含有其他各元的项的系数均为零而成为一元方程的情形。例如x+1=0可看成x，y的二元方程x+0y+1=0，它在平面直角坐标系中表示一条直线1。

基本介绍在数域F上只含有一个未知数的方程，叫做F上的一元方程，一元一次方程、一元二次方程等都是一元方程。一元方程的解又叫做方程的根。

含有未知数的等式叫做关于这个(或这些)未知数的方程，简称方程。方程中的未知数叫做方程的元。含有几个未知数的方程就叫做几元方程。例如，关于x的方程ax=b，就是以x为未知数的一元方程。等式F1(x，y，z)=F2(x，y，z)就表示一个以x，y，z为元的三元方程。

一元方程的解与解集能够使方程左右两边的值相等的未知数的值，叫做方程的解。多元方程的解是一组未知数的值。如x=2，y=1是二元方程2x-y=3的一个解2。

一元方程的解也叫做方程的根。如果一个方程的全体根中有几个根相等，那么这几个根叫做重根。例如一元方程x3(x-1)2(x+3)=0，它的根是x1=x2=x3=0，x4=x5=1，x6=-3，那么“0”就是它的三重根，“1”就是它的二重根，“-3”不是重根，可以称之为单根，一般只对整式方程研究重根问题。

一个方程的解的全体所组成的集合，叫做这个方程的解的集合，简称解集。若方程无解，解集就是空集。无解的方程叫做矛盾方程，故矛盾方程的解集是空集2。

求出方程的所有的解或判断方程无解的过程，叫做解方程。在不同的数集里解同一个方程，所得的解集不一定相同。例如一元方程

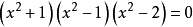在有理数集里有两个根是±1，其解集是{1，-1};在实数集里有四个根是

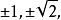那么在实数集里解此方程所得解集为

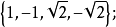在复数集里解此方程则有六个根：

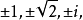故得解集为

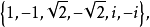再如方程

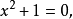在实数集里是矛盾方程，在复数集里则不是矛盾方程。一般地，应指明在什么范围(数域)里研究。中学数学里解方程时若不明确求解的范围(数域)，即是指在实数域里求解2。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学