[科普中国]-多变量平稳时间序列

一串按时间顺序排列的反映某一特定内容的数据叫做时间序列。同时表明多项指标的时间序列称作多变量时间序列。若多变量时间序列滞后r 步的协差阵与t无关，则称多变量序列是多变量平稳时间序列。1

定义时间序列：一串按时间顺序排列的反映某一特定内容的数据。用 表示时间序列，其下标整数变量 代表等间隔的时刻，例如表示第 天、第 月、第 季、第 年等。1

在统计中对每一个特定时刻 的数据 看作是一个随机变量。在实际进行统计时不可能在无限长度的时间区间进行观察，只能在有限的时间间隔对某一现象进行观察，因此所取得的观察值是时间序列的一串有限个样本值。一般将时间序列记为 ，其中 是观察的终止时刻，时间序列分析的目的是发现数值变化的规律性，建立适当的数学模型，起到预测和控制等作用。1

多变量时间序列：同时表明多项指标的时间序列 称作多变量时间序列。虽然把各项指标分别看作是单变量序列来研究，这也能提供各个序列所包含的信息，但却不能揭示这些序列之间可能存在着的相互关系，因此需要有描述多变量序列的一些二阶联合特性，如互相协方差、互相关函数，互谱以及相应的多变量ARMA模型。1

多变量平稳时间序列：设 为多变量时间序列滞后 步的协差阵，其中 当 时 表示序列 的自协方差函数； 时 表示序列 和 之间的互协方差函数。若对所有 仅是 的函数(与 无关)，则称多变量序列是联合平稳的，或简称为平稳的。1

性质时间序列分析主要是针对平稳的时间序列，有些时间序列是非平稳的，但经过差分后可以得到一个平稳序列。设 是非平稳序列，但经一阶差分后得到的序列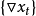 可能是平稳的。有时可能经若干阶差分后才能平稳化。对于这类序列，称为自回归—求和—移动平均模型，或称ARIMA模型。1

举例在现实中很多问题，如利益波动、收益率变化及汇率变化等通常是一个平稳序列，或者通过差分等变换可以化成一个平稳序列。2

应用一个平稳序列的行为不会随时间的推移而变化，因此，可以用该序列过去的行为来预测它的未来。这是随机时间序列模型的优势所在。2

对于一个平稳的时间序列，可以采用自回归AR模型、移动平均MA模型和自回归移动平均ARMA模型进行分析。2

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学