若平稳时间序 适合于ARMA(p,q)模型,则其自相关函数,偏相关函数都是按负指数衰减,这一特点是由ARMA模型相应的线性差分方程的性质所决定,通常称这种特性为拖尾性,因此实践中可用来对模型进行识别。1
定义若平稳时间序列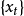 适合于
适合于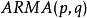 模型,则其自相关函数,偏相关函数都是按负指数衰减,这一特点是由
模型,则其自相关函数,偏相关函数都是按负指数衰减,这一特点是由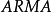 模型相应的线性差分方程的性质所决定,通常称这种特性为拖尾性,因此实践中可用来对模型进行识别。1
模型相应的线性差分方程的性质所决定,通常称这种特性为拖尾性,因此实践中可用来对模型进行识别。1
性质设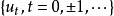 为实序列,满足齐次线性差分方程
为实序列,满足齐次线性差分方程
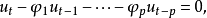 差分方程相应的特征方程为
差分方程相应的特征方程为 ,设其根为
,设其根为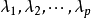 。其自相关函数
。其自相关函数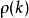 当
当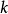 充分大时也满足上述差分方程,故可表示为特征根
充分大时也满足上述差分方程,故可表示为特征根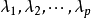 次幂的线性组合。1
次幂的线性组合。1
若 ,则具有平稳解。若特征根皆实根,则
,则具有平稳解。若特征根皆实根,则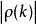 依
依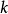 单调衰减;若存在单位圆内的复根,则呈共轭对出现,方程通解中含正弦余弦项,
单调衰减;若存在单位圆内的复根,则呈共轭对出现,方程通解中含正弦余弦项,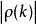 呈振荡式衰减,其典型图形如下:1
呈振荡式衰减,其典型图形如下:1
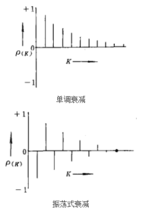
应用-格林函数预报法格林函数预报法是平稳时间序列的一种直接预报方法。设观察序列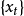 为
为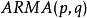 模型,
模型,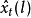 表示在
表示在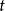 时刻对未来
时刻对未来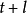 时刻的值
时刻的值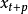 所作的平稳线性预报,则格林函数预报法由模型参数递推计算格林函数
所作的平稳线性预报,则格林函数预报法由模型参数递推计算格林函数
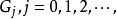 然后
然后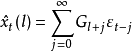 ,取值
,取值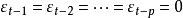 ,
,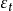 可按
可按
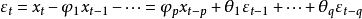 递推计算。该公式包含无穷项求和,实际上只可能用充分多项的有穷和近似,即
递推计算。该公式包含无穷项求和,实际上只可能用充分多项的有穷和近似,即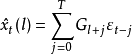 。由
。由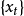 的平稳性保证了
的平稳性保证了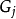 是负指数衰减的,当
是负指数衰减的,当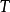 充分大时,
充分大时,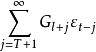 小于给定精度。1
小于给定精度。1
本词条内容贡献者为:
任毅如 - 副教授 - 湖南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国