[科普中国]-幂指方程

诸如xx=x这样的方程，既不是整式方程，又不是指数方程，更一般地，如果在方程中出现底数和指数中同有未知数的项，这样的方程通常叫做幂指方程(power-exponent equation)。幂指方程的求解甚为复杂，通常讨论如下两种简单情形：限于寻求整数解；底数虽有未知数，但取值恒为正数1。

基本介绍幂指方程是一种特殊的指数方程，指在方程中出现乘幂且底数与指数中同时含有未知数的方程，例如xx=x(x>0)。幂指方程的求解较为复杂，通常只讨论如下两种简单情形：限于求整数解；作为底数的未知数的函数式恒取正值。例如，解方程

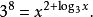
由log3x知x>0，且方程的右边在(0，+∞)上有意义，对方程的两边取以3为底的对数得

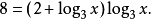
令y=log3x，得8=(2+y)y。解之有y1=-4，y2=2，即log3x=-4或log3x=2，所以原方程的解为x1=1/81，x2=92。

指导 关于幂指方程的一般解法(分三步) : ①讨论确定x的允许取值范围；②讨论底数为0，±1时的情况，适合者为根；③在x的允许取值范围内，且在x≠0，±1的条件下，按一般指数方程解之。见下文例1。

举例说明【例1】解方程:。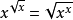

解：第一步:确定x的允许取值范围3。

由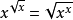知，如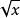有意义，必须x≥0，

又∵0º无意义，

∴x≠0，因此，x> 0。

第二步:讨论底数。

显然x= 1适合方程。

第三步:在x>0，x≠1的前提下，

由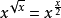得：

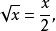解得:

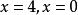(不适合，舍去)

原方程的解为: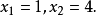

【例2】解方程:。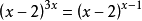

解 (1) 当x-2