[科普中国]-闪锌矿晶体

闪锌矿晶体是立方晶系的晶体，并且都具有面心立方Bravais格子，晶胞和原胞的形式也都相同，晶体中有两种不同元素的原子。GaAs等大多数Ⅲ-Ⅴ族化合物半导体和一些重要的Ⅱ-Ⅵ族化合物半导体都具有闪锌矿型的晶体结构。

概念闪锌矿晶体(β-ZnS)属等轴晶系，间群为T2d-F-43m，晶体中锌离子分布于晶胞的角顶和面心，将晶胞分成八个小立方体，硫离子位于相间的四个小立方体的中心。晶体的结构单元是Zn-S4四面体，根据负离子配位多面体生长基元模型，闪锌矿晶体的生长基元为Zn-S4四面体以及多个Zn-S4四面体以顶点相连的具有不同几何结构的锌硫离子团。

晶体生长基元的稳定能与闪锌矿的结晶形态材料科学的发展和现代科技的需求，促使人们对许多晶体进行了人工生长研究，有的已经进行工业化生产。在长期的人工晶体生长的实践中，人们发现许多实验事实不能简单地套用经典的晶体生长理论来解释。我国晶体科学工作者在大量的晶粒制备实验基础上，形成和发展了“负离子配位多面体生长基元”理论模型。它认为在低受限晶体生长系统(如水热晶体生长系统，高温溶液晶体生长系统等)中，溶质相互作用或者溶质与溶剂相互作用，形成具有一定几何构型的聚集体，即生长基元。同一反应体系中存在多种形式的生长基元，它们之间建立起动态平衡。生长基元的稳定性可以用基元稳定能加以描述，相对较为稳定的生长基元称之为有利基元，有利生长基元的基本结构单元与相应的晶体的结构单元一致。研究从负离子配位多面体生长基元模型出发，建立了闪锌矿晶体生长基元的数学模型，通过对闪锌矿晶体生长基元稳定能的计算，讨论了闪锌矿的结晶形态和生长机理。

硫化锌晶体生长基元的数学模型和稳定能为了计算闪锌矿晶体的具有不同几何结构的生长基元的稳定能，先给出表示闪锌矿晶体生长基元的格点图。在空间直角坐标系或仿射坐标系中，当x，y，z均为整数时，称点P(x，y，z)为格点。设G为一有限连通图，如果G的n个结点(ν1，ν2，…，νn)均为格点，而且，e=(νi，νj)是G的边的充分必要条件，那么：xj-xi+yj-yi+zj-zi=1，其中，(xi，yi，zi)和(xj，yj，zj)分别为νi和νj的坐标，则称G为格点图。对闪锌矿晶体的任一生长基元，将坐标原点O取在其中一个锌硫四面体的锌离子处，取三个基向量e1，e2，e3分别平行于该四面体不共面的三个S-S键，使其两两间的夹角等于π/3，单位长度等于S-S键长，则在空间仿射坐标系[O，e1，e2，e3]中，生长基元中的所有锌离子均占据而且仅占据一些格点。若将生长基元中锌离子所占据的格点作为结点，以所有坐标满足xj-xi+yj-yi+zj-zi=1的结点νi和νj的连线为边[其中，(xi，yi，zi)和(xj，yj，zj)分别为结点νi和νj的坐标]，如此构成的图就是生长基元的格点图。

计算结果及讨论M个锌硫四面体可以形成多种几何结构的生长基元，在同一反应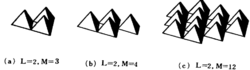体系中存在多种形式的生长基元，它们之间建立起动态平衡。生长基元的稳定性可以用基元稳定能加以描述，相对较为稳定的生长基元称之为有利基元。通过计算各种几何结构的生长基元的稳定能，可以从定量的角度探讨反应体系中何种几何结构的生长基元为有利基元。首先讨论直链状生长基元，图1给出了一些直链状生长基元的示意图。表1是直链状生长基元的稳定能U的计算结果，其中M表示锌硫四面体的个数。计算结果表明，随着链长的增加，稳定能急剧减小，因此，反应体系中很难形成直链状生长基元。考虑平面状生长基元的情况，图2给出了一些锌硫四面体构成的等边平面状生长基元的示意图。表2给出了锌硫四面体构成的等边平面状生长基元(如正三角形、正六边形和平行四边形形状生长基元)稳定能U的计算值，其中L值指生长基元边长被锌硫四面体的S-S键长整除所得的商。计算结果表明，无论是正三角形、正六边形还是平行四边形形状的生长基元，稳定能U都随基元直径的增大(M数的增加)而单调减小，因此，生长体系中也难以形成等边平面状生长基元。

考虑锌硫四面体构成柱状生长基元的情形，若干个由锌硫四面体组成的L数相同的平面正三角形基元沿其法线方向往上键合，叠合形成柱状生长基元，可以有正三角斜柱状或正三角直柱状生长基元，图3是两个正三角斜柱状和正三角直柱状生长基元的示意图。类似还可有四方斜柱状或四方直柱状、正六边斜柱状或正六边直柱状生长基元。表3给出了它们的稳定能U的计算值，它们的稳定能U都随基元层数的增加(M数的增加)而减小，因此，生长体系中也难以形成这些类型的生长基元。边长为L的正三角形形状基元若按斜柱状往上叠合，每往上一层，L值减1，直至L等于1为止，可构成大的边长为L的正四面体状生长基元，图4是一些正四面体状生长基元的示意图。表4给出了L取不同值时正四面体状生长基元的稳定能U的计算值。计算结果表明，随着正四面体生长基元边长L的增加，稳定能单调增大，说明正四面体状生长基元是闪锌矿晶粒的有利生长基元。

根据以上计算结果，可以对闪锌矿晶粒的形成过程作如下描述：在反应体系中，由于不同区域中能量的起伏和离子浓度的涨落，可以形成各种几何结构的生长基元，然而为了追求最大稳定能，仅有上述边长为L的正四面体形的有利基元才能较长久地存在，L值越大，存在的时间越长，也越容易长大，它们是闪锌矿晶体的晶胚。以热力学为基础的经典晶体成核和生长理论认为：当体系中离子团的离子数超过成核临界值时，即可形成稳定的晶核并且逐渐长大。

因此，随着L值的增大，当该正四面体形生长基元中的离子个数超过成核临界值时，即可形成稳定的闪锌矿晶核，并且在适宜的条件下逐渐长大，最后形成正四面体形的闪锌矿晶粒，这就说明了闪锌矿晶体可具有正四面体形结晶形貌。1

飞秒激光激励闪锌矿晶体太赫兹辐射分析飞秒激光激励闪锌矿晶体产生太赫兹辐射，其原理是一个基于非线性效应的光整流过程。这种太赫兹源的方法实现起来简单方便，但发射效率不高；由于晶体中的光整流过程与晶体的二阶非线性极化系数张量和参与非线性过程的电场强度矢量有关，因此晶体的晶向选择和入射激励光的电场偏振方向对太赫兹的产生效率有重要影响，研究人员对这个问题已经有了一些研究成果，但缺少完全的、系统化的描述，文章对这一问题进行了详细完备的数学分析，计算了太赫兹辐射最优化的晶体晶向选择以及激励光的入射角度和偏振方向，系统地阐述了晶体晶向、激励光入射角和电场偏振方向对太赫兹辐射的影响。

激励光斜入射下的太赫兹产生在很多场合，激励光并不是正入射的，而是以一定的入射角进入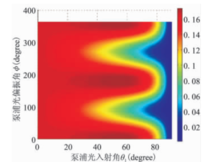晶体，因此入射角的选择对太赫兹的辐射强度同样具有影响。当激励光斜入射晶体上时，在原本最优晶向位置，太赫兹强度峰值向两侧漂移，形成双峰图样。且随着入射角的增大，这种漂移越明显，但总体来说，漂移角度不大，并且太赫兹辐射强度的起伏也不大，因此斜入射与正入射都可以使用同样的最优晶向。

从图5中可以看出，当θ1=0即正入射情况下，入射光的偏振方向并不改变能获得的最大太赫兹辐射场的大小，因为太赫兹场与入射光的偏振方向与晶体方位角θ的差值有关，即便取不同的偏振角，也可以通过调整晶体方位角的大小来使辐射的太赫兹场取恒定最大值；而随着入射角度的增加，入射光偏振方向对能获得的最大太赫兹辐射影像增强，只有在入射光偏振角为0°、180°时，即入射光电场偏振方向在入射面xz平面内时，太赫兹辐射场才能获得最大值，这就意味着入射光应选择p偏振。另外，随着入射角的增加，所能获得的最大太赫兹辐射场逐渐增加到最大值然后迅速减小并最终消失，最优入射角由晶体的折射率参数决定。

研究结论建立了基于光整流机制产生太赫兹辐射的详细数学描述，讨论了激励光入射角度、偏振状态、晶体晶向及晶体方位角等参数对所能获得的最大太赫兹辐射场的影响，获得了几点结论:首先不管正入射还是斜入射，最优晶向都不是单一的，但选择晶向是适宜的；正入射时，太赫兹辐射场受入射光偏振方向与晶体方位角的夹角影响，在任意偏振方向下可以通过旋转晶体获得最大的太赫兹辐射，但在斜入射时，入射光偏振方向需要在入射面内，并且斜入射相比于正入射可以获得更高的太赫兹辐射强度。2

本词条内容贡献者为:

程鹏 - 副教授 - 西南大学