[科普中国]-n次单位根

n次单位根(n-th unit root)是一种重要的n次方根，数1在复数范围内的n次方根，称为n次单位根，简称单位根。由此可知，所谓n次单位根，也就是多项式xn－1或方程xn－1=0在复数域内的根1。

基本介绍在复数范围内，1的n(n∈N)个不同的n次方根都称为n次单位根，简称单位根。它们是

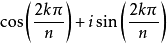或

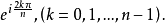
n次单位根是方程ωn-1=0的n个不同的根，除ω0=1外，其余n-1个也是n-1次方程ωn-1+ωn-2+…+ω+1=0的n-1个不同根2。

n次单位根的性质n次单位根有下列性质2：

1.对于任何m∈Z

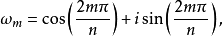或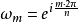都是n次单位根，即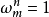，但不同的单位根只有n个。例如取m=0，1，2，…，n-1时，就得到n个不同的n次单位根。当整数m=qn+k(q∈Z+，k∈{0，1，2，…，n-1})时，ωm=ωqn+k=ωk。

2.n次单位根的模为1，即|ωm|=1。

3.两个n次单位根ωi，ωj的乘积仍是一个n次单位根，且ωi·ωj=ωi+j(i，j为任意整数)。由此可得：

1) (ωi)-1=ω-i。

2) (ωk)m=ωmk(m，k为任意整数，当m=0时，(ωk)0=1=ω0)。

3) ωk=ωl的充分必要条件是k与l除以n后余数相同，即k与l的差是n的倍数。

4) 任何一个单位根都可以写成ω1的幂，如ωk=(ω1)k，有这种性质的n次单位根ω1称为n次本原单位根，简称n次原根或原根，当p与n互素且1≤p