[科普中国]-诱导比例

诱导比例(induced proportion)是比例的一种恒等变形，对于一个已知比例的某些项，施行某些运算，可以得到一些新的比例，这些新的比例叫做从已知比例得到的诱导比例。例如：合比定理、分比定理、合分比定理、等比定理、连比定理等，都是诱导比例1。

基本介绍诱导比例是比例的一种恒等变形，对于一个已知比例的一些项施行若干运算而得出一些新比例，称为已知比例的诱导比例。从已知比例a/b=c/d可得下列诱导比例2：

1.第一个比的两项之和(或差)比其后项，等于第二个比的两项之和(或差)比其后项，即

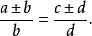
2.第一个比的两项之和(或差)比其前项，等于第二个比的两项之和(或差)比其前项，即

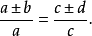
3.第一个比的两项之和比它们的差，等于第二个比的两项之和比它们的差，这称为合分比定理，即

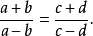
4.从上述性质1，2和3再利用更比定理和反比定理，尚可得出下列诱导比例2：

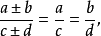
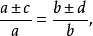
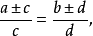
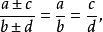
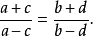
相关介绍在所有的比例中，它的两个外项的积等于两个内项的积。这叫做比例的基本性质。用式子表示这一性质，就是：

如果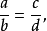 (a、b、c、d都不等于零)

那么ad= bc。

证明用bd去乘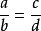 的两边，即

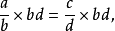所以，ad= bc。

下面分析一下ad=bc的诱导比例3****。

由此性质可以推出：

如果两个数的乘积等于另外两个数的乘积，那么这四个数成比例(也就是可以组成比例)。用式子表示，就是

如果ad=bc，那么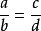3。

证明用bd去除ad=bc两边，即

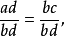得

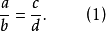我们还可以分别用cd、ab、ac去除ad=bc两边，得到不同的比例：

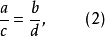
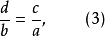
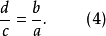
如果把(1)、(2)、(3)、(4)四个比例的左右两边对调，那么又可以得到四个比例：

由此可以看出，如果两个数的积等于另外两个数的积，那么这四个数就可以组成八个比例。这八个比例的形式不同，也就是各个数在比例中的位置不同。这八个比例叫做ad=bc的诱导比例3。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所