[科普中国]-广义费马定理

广义费马定理是费马定理的一种推广。实则把费马小定理从整数范围推广到整系数多项式的集合中而得到。

简介广义费马定理是费马定理的一种推广。设p为素数，φ(x)为n次不可约多项式mod p，则对任何一个非φ(x)之倍式的多项式f(x)，mod p，恒有

对任一多项式常有特别有，此即称为广义费马定理，实则把费马小定理从整数范围推广到整系数多项式的集合中而得到。

推论广义费马定理有下述推论：

1.任何一个n次不可约多项式必能整除。此性质可由广义费马定理直接推出。

2.重模方程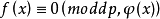之根数不超过f(x)的次数，这里f(x)表整系数多项式。

3.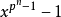不能被一个次数高于n次的不可约多项式所整除mod p。

4.若Ψ(x)为一个l次不可约多项式，mod p，且，则l|n。1

费马小定理费马小定理是数论中的一个重要定理，1636年提出.

费马小定理的内容为：假如p是质数，且gcd(a,p)=1，那么ap-1≡1(mod p)，例如：假如a是整数，p是质数，则a,p显然互质（即两者只有一个公约数1），那么我们可以得到费马小定理的一个特例，即p为质数时，ap-1≡1(mod p)。

费马小定理是初等数论四大定理（威尔逊定理，欧拉定理（数论中的欧拉定理），中国剩余定理（又称孙子定理）之一，在初等数论中有着非常广泛和重要的应用。实际上，它是欧拉定理的一个特殊情况（即）。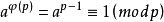

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所