[科普中国]-平行平面截直线定理

平行平面截直线定理，是指两条直线穿过一组平行平面，则其各平面的交点所组成的线段成比例的一个立体几何定理。

简介平行平面截直线定理是立体几何的重要定理之一。

如果α1，α2，...，αn是一组平行平面，直线a，b都与它们相交，其交点分别为A1，A2，...，An与B1，B2，...，Bn（如图），则对任何i,j,k,l∈{1,2,...,n},i≠j,k≠l，有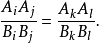

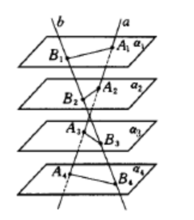
两平行平面的判定下列条件每一个都可判定两平面平行：

1、一个平面内有两条相交直线都平行于另一个平面。

2、都垂直于同一条直线。

3、都平行于第三个平面。

4、一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行。

两平行平面的性质两平行平面的主要性质有：

1、它们和第三个平面的交线平行。

2、垂直于一个平面的直线也垂直于另一个平面。

3、和其中一个平面相交的直线必和另一个平面相交。

4、第三个平面和其中一个平面相交（或平行），必和另一平面也相交（或平行）。

5、其中一个平面上的任何一条直线都平行于另一个平面。

6、夹在它们间且与它们相交的平行线段相等；公垂线段的长相等。1

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所