谢尔品斯基猜想(Sierpiski conjecture)是关于单位分数的著名猜想。该猜想可表述为:当n较大时,真分数m/n 能表示成三个单位分数(不一定相异)的和。1
谢尔品斯基猜想谢尔品斯基猜想(Sierpiski conjecture)是关于单位分数的著名猜想。该猜想可表述为:当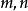 为正整数,
为正整数,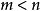 ,且
,且 较大时,不定方程
较大时,不定方程
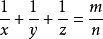 一定有正整数解。1
一定有正整数解。1
古埃及的兰德纸草书上就记载了用单位分数 表示真分数的方法。后来知道任何真分数
表示真分数的方法。后来知道任何真分数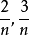 都能表为两个或三个相异的单位分数的和:
都能表为两个或三个相异的单位分数的和:
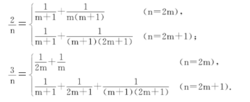
1950年,爱尔特希(Erdo¨s,P.)猜想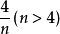 能表示成三个相异的单位分数的和。
能表示成三个相异的单位分数的和。
谢尔品斯基(Sierpiski,W.)猜想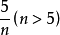 也能表示成三个单位分数的和。
也能表示成三个单位分数的和。
谢尔品斯基还进一步猜想:在 较大时,真分数
较大时,真分数 都能表示成三个单位分数(不一定相异)的和,即上述不定方程有正整数解。这里要限定
都能表示成三个单位分数(不一定相异)的和,即上述不定方程有正整数解。这里要限定 较大,是因为
较大,是因为 较小时发现有猜想不成立的例子。比如已证明
较小时发现有猜想不成立的例子。比如已证明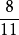 至少需要4个单位分数的和才能表示它。至今还未能证明上述猜想是否成立。1
至少需要4个单位分数的和才能表示它。至今还未能证明上述猜想是否成立。1
有关欧拉函数的谢尔品斯基猜想所谓欧拉函数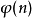 指的是,在
指的是,在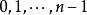 中与
中与 互素的整数的个数。有关欧拉函数取值的谢尔品斯基猜想表述如下:
互素的整数的个数。有关欧拉函数取值的谢尔品斯基猜想表述如下:
设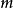 为一给定的正整数,它可以作为
为一给定的正整数,它可以作为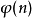 值出现的次数,即满足
值出现的次数,即满足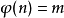 的不同的正整数
的不同的正整数 的个数,称为整数
的个数,称为整数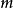 的重数。2
的重数。2
例如,6的重数是4,这是因为当且仅当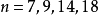 时,
时,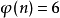 成立。由于对于
成立。由于对于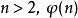 均为偶数,故对于所有大于1的奇数
均为偶数,故对于所有大于1的奇数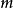 ,它们的重数都是0。重数为0的偶数有
,它们的重数都是0。重数为0的偶数有
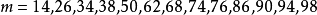 等。它们都是使方程
等。它们都是使方程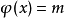 没有整数解
没有整数解 的
的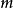 。在小于
。在小于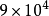 范围内,这样的偶数有26663个。2
范围内,这样的偶数有26663个。2
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国