逐步淘汰原则(successive sweep principle )亦称容斥原理,这是数论和组合理论的重要方法。在数论中,常常遇到一些计数问题,这些计数问题往往归结为计算一个有限集S中不属于某些指定子集的元素的个数。应用逐步淘汰原则,可以很容易得到计算欧拉函数的重要公式。1
定义设 是一个非空的含有有限多个元素的集合,
是一个非空的含有有限多个元素的集合, 为一个正整数,
为一个正整数,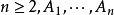 是
是 的
的 个子集。若以
个子集。若以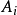 表示
表示 中具有性质
中具有性质 的元素全体构成的集合,则可知:在
的元素全体构成的集合,则可知:在 中既不具有性质
中既不具有性质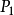 ,又不具有性质
,又不具有性质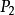 ,...,又不具有性质
,...,又不具有性质 的元素的个数为
的元素的个数为

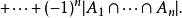 上述计数表达式通常被称为逐步淘汰原则(或容斥原理)。2
上述计数表达式通常被称为逐步淘汰原则(或容斥原理)。2
证明我们用 表示任一个有限集合
表示任一个有限集合 中元素的个数。若
中元素的个数。若 为空集,则令
为空集,则令 。
。
设 是一个非空的含有有限多个元素的集合,
是一个非空的含有有限多个元素的集合, 为一个正整数,
为一个正整数,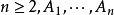 是
是 的
的 个子集,则可以证明
个子集,则可以证明
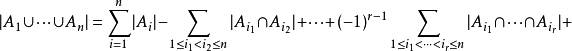
 上式可以从相应于
上式可以从相应于 时的关系式(
时的关系式( 与
与 为
为 的任意子集)
的任意子集)
 经应用数学归纳法而获得证明。
经应用数学归纳法而获得证明。
若用 表示
表示 的任一子集
的任一子集 在
在 中的余集(即
中的余集(即 是由
是由 中的不在
中的不在 中的元素构成的),则有
中的元素构成的),则有
 现在,若以
现在,若以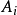 表示
表示 中具有性质
中具有性质 的元素全体构成的集合,则可知:在
的元素全体构成的集合,则可知:在 中既不具有性质
中既不具有性质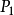 ,又不具有性质
,又不具有性质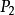 ,...,又不具有性质
,...,又不具有性质 的元素的个数为
的元素的个数为

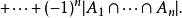 2
2
举例例如,若 表示正整数,
表示正整数,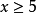 ,集合
,集合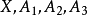 定义为
定义为

 则不超过
则不超过 且既不能被3除尽,也不能被5除尽的正整数的个数为(注意:
且既不能被3除尽,也不能被5除尽的正整数的个数为(注意: )
)
 2
2
Euler函数的计算公式应用逐步淘汰原则,就很容易得到计算欧拉函数 的重要公式。
的重要公式。
Euler函数的定义:模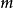 的同余类
的同余类 称为是模
称为是模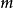 的既约 (或互素)同余类,如果
的既约 (或互素)同余类,如果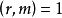 。模
。模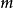 的所有既约同余类的个数记作
的所有既约同余类的个数记作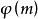 ,通常称为Euler函数。3
,通常称为Euler函数。3
定理3 若 是不同的素数,则
是不同的素数,则
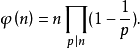
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国