[科普中国]-广义素数定理

广义素数定理(generalized prime number theorem)是素数定理的推广，广义素数定理是1982年爱尔特希(P.Erdös)提出和证明的。素数定理指素数出现的规律，可分为自然数素数定理、函数素数定理及广义素数定理等，“自然数素数定理”和“函数素数定理”可统称为狭义素数定理1。

基本介绍设整数n>1，P(n)表n的最大素因子，p(n)表n的最小素因子，则有

S(x)=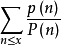 =(1+o(1))π(x)； (1)

S(x)=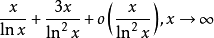 ； (2)

当n仅取素数时，

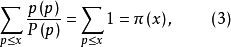
所以，S(x)是π(x)的一种推广。而(1)表明S(x)与π(x)是等价的，(3)式则进一步求出了S(x)的渐近公式，但注意到对任意正整数A，由于有

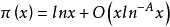
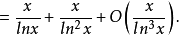因而S(x)与π(x)进一步的渐近公式是不同的，S(x)最好的结果是

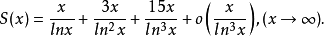通过复杂的计算，还可以定出此渐近公式中的更低次项。但是，是否存在一个函数f(x)，使对任意的正整数A，有S(x)=f(x)+O(x ln-Ax)，迄今尚未解决2。

相关介绍定义1 素数定理指素数出现的规律，可分为自然数素数定理、函数素数定理及广义素数定理等，每种素数定理，又分为实际素数定理和理论素数定理等，这里说的规律包括某范围的概率分布函数、素数个数、均方差及边界等量的集合，它将目前说的“素数定理”的概念进行了扩展，其中，自然数素数定理是函数素数定理的特例，函数素数定理是自然数素数定理的推广，故“自然数素数定理”和“函数素数定理”可统称为狭义素数定理1。

定义2 在t≤N内的函数或条件H(t)中，出现狭义或广义素数的规律，定义为狭义或广义素数定理，H(t)的素数率记为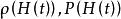 ，素数个数实际值及理论值分别表为π(H(N))及Π(H(N))，则

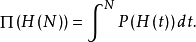在素数定理中，当具有特征量x时，它们的个数可记为π(N,x), Π(N,x)，它们的归一化概率分布函数可记为ρ(N,x)，P(N,x)， 则1

π(N,x)=π(N)ρ(N,x)

Π(N,x)=Π(N)P(N,x)

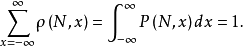
爱尔特希爱尔特希(P.Erdös)是匈牙利数学家。犹太人。生于布达佩斯，是两位中学数学教师的独子，一个数学神童，3岁时已能心算三位数的乘法，4岁时便发现了负数。1930年进入布达佩斯大学学习数学，1934年毕业并获得博士学位。1934年10月，赴英国曼彻斯特，从事为期4年的博士后研究。之后不间断地旅行了50多年，从未在一个地方停留一个月以上，没有妻小，没有职业，没有其他嗜好，完全献身于对美妙的数学问题和新奇的数学技巧的追求之中，以近乎疯狂的节奏，奔波于四大洲一个又一个大学或研究中心。他是匈牙利科学院院士，荷兰皇家研究院院士，以及伦敦数学会、美国数学会会员3。

爱尔特希的数学兴趣包括数论、集合论、组合数学、图论、概率论及其应用以及数理逻辑等。尤其在数论方面的工作最为突出，被誉为“一心迷恋于数的学者”。在整数分析问题的研究中，17岁时他便给出了“在任何一个(大于1的)整数和它的两倍数之间必定存在素数”的一个简单证明，轰动了匈牙利数学界。1942年，他用初等的函数论方法估计了n的分拆数p(n)的值。还提出了一个猜想：如果n个等差数列没有覆盖住自然数列，那么必存在0