[科普中国]-维格纳-埃卡特定理

维格纳-埃卡特定理（英语：Wigner–Eckart theorem）为量子力学中表示论的一个定理。 这个定理说明，在角动量本征态的基底下， 球张量（spherical tensor）算符的矩阵元素可以写作两个部分的乘积。 一部分与角动量无关，而另一部分为Clebsch-Gordan系数。 这个定理的名称来自发展这些计算推导的两位物理学家：尤金·维格纳和卡尔·埃卡特。 他们将薛定谔方程式中的对称群与能量、动量、角动量的守恒用数学公式连结起来。

简介维格纳-埃卡特定理（英语：Wigner–Eckart theorem）为量子力学中表示论的一个定理。 这个定理说明，在角动量本征态的基底下，球张量（spherical tensor）算符的矩阵元素可以写作两个部分的乘积。 一部分与角动量无关，而另一部分为Clebsch-Gordan系数。 这个定理的名称来自发展这些计算推导的两位物理学家：尤金·维格纳和卡尔·埃卡特。 他们将薛定谔方程式中的对称群与能量、动量、角动量的守恒用数学公式连结起来。

维格纳-埃卡特定理如下：

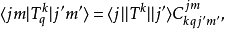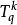当中是一个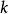阶的球张量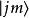，和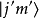为总角动量与 z-方向角动量的本征态。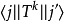代表一个与量子数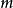、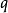无关的值。为Clebsch-Gordan系数。1

表示论表示论是数学中抽象代数的一支。旨在将抽象代数结构中的元素“表示”成向量空间上的线性变换，并研究这些代数结构上的模，藉以研究结构的性质。略言之，表示论将一代数对象表作较具体的矩阵，并使得原结构中的代数运算对应到矩阵加法和矩阵乘法。此法可施于群、结合代数及李代数等多种代数结构；其中肇源最早，用途也最广的是群表示论。设G为群，其在域F（常取复数域 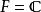）表示是一F-矢量空间V及映至一般线性群之群同态

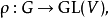
假设V有限维，则上述同态即是将G的元素映成可逆矩阵，并使得群运算对应到矩阵乘法。

表示论的妙用在于能将抽象代数问题转为较容易解决的线性代数问题。此外，群还可以表示在无穷维空间上；例如，若考虑无穷维希尔伯特空间上的表示，并要求一些连续性条件，此时表示论就牵涉到一些泛函分析的课题，数学分析的方法就可以用于解决群论的问题。表示论在自然科学中也有应用。对称性的问题离不开群，而群的研究又有赖于其表示，最明显的例子便是李群及李代数表示论在量子力学中的关键角色。

表示论的一大特点是它遍布数学各个领域。这个特点有两个方面。首先，表示论的应用十分广泛：除了在代数的影响之外，表示论

通过调和分析阐明并推广了傅里叶分析，

通过不变量理论和爱尔兰根纲领与几何学建立了联系

通过自守形式和朗兰兹纲领对数论产生了影响。

另一方面，研究表示论的途径也相当多元化，应用了代数几何、模论、解析数论、微分几何、算符理论、代数组合学和拓扑学的思想和方法

“表示”的概念后来也得到进一步的推广，例如范畴的表示。表示论所施的代数对象可被视为特定的范畴，而表示本身则是从对象范畴到向量空间范畴的函子。这个表述方式立即指向两种显然的推广：其一，代数对象可换成成更一般的范畴；其二，向量空间范畴也可换成其它较好理解的范畴。2

另见表示

表示定理

伽罗瓦表示

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所