[科普中国]-二项同余方程

二项同余方程(binomial congruence equation)亦称二项同余式，是一类特殊的同余方程，设k≥1，同余方程xk≡a(mod m)，(a，m)=1被称为是模m的二项同余方程1。

基本介绍设整数k≥1，正整数m的标准分解式为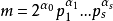，而形如

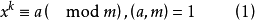的同余式称为二项同余方程，它等价于下面二项同余方程组

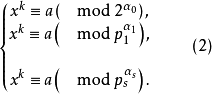
利用原根的最小指数表可以解出(2)中的每一个同余方程。若(1)有解，则称a为模m的k次剩余；若(1)无解，则称a为模m的k次非剩余。a是模m的k次剩余的充分必要条件是a为每一个模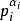(i=1，2，…，s)的k次剩余，因此，(1)若有解，则根据孙子定理可归结为解形如

的二项方程2。

二项同余方程的解关于二项同余方程(1)的解有如下结论：

1.设m>1，且有原根 ɡ，(a，m)=1，k≥1，则(1)有解的充分必要条件是(k，φ(m))|ind a，若有解，恰有(k，φ(m))个解。

2.设m>1，k≥1，(a，m)=1，模m有原根，则a是模m的k次剩余的充分必要条件是

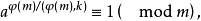且模m的k次剩余的个数为φ(m)/(φ(m)，k)。

3.若m=2α，α≥3，2∤a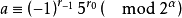，，则二项同余方程xk≡a(mod 2α)当2∤ k时恰有一解；当2|k时有解的充分必要条件是r-1=0，且(k，2α-2)|r0，若有解，恰有2(k，2α-2)个解2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所