[科普中国]-狄利克雷逆

狄利克雷逆(Dirichlet inverse)是数论函数的重要运算之一，即狄利克雷乘积的逆运算。设f(n)为数论函数，若存在数论函数g(n)，使得f*g=I，则称g(n)为f(n)的狄利克雷逆，或简称逆，记为f-1(n)=g(n)。

基本介绍设f(n)为数论函数，若存在数论函数g(n)，使得f*g=I，则称g(n)为f(n)的狄利克雷逆，或简称逆，记为f-1(n)=g(n)。例如，μ*U=I，故U(n)的逆μ-1(n)=U(n)≡1。反之，U(n)≡1的逆U-1(n)=μ(n)，从定义及交换律可知，若g为f的逆，则f亦为g的逆，即若g=f-1，则f=g-1。

狄利克雷逆的性质狄利克雷逆有下述性质：

1.若数论函数f(n)满足f(1)≠0，则存在惟一的逆f-1(n)，且满足

f-1(1)=1/f(1)，

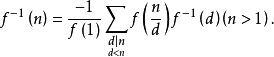
故知积性函数f必有逆f-1，且f-1仍为积性函数。

2.若数论函数f(n)，g(n)满足f(1)≠0，g(1)≠0，则(f*g)-1=f-1*g-1。

3.若f(n)为积性函数，则f(n)为完全积性函数的充分必要条件是f-1(n)=μ(n)f(n)。特别地，当g(n)为完全积性函数，且h=f*g时，有f=h*μg1。

重要的狄利克雷逆重要的狄利克雷逆有：

设，则

特别地，当λ=0或1时，得到

及

2.设φ(n)为欧拉函数，则.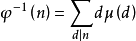

3.默比乌斯函数μ(n)的逆μ-1(n)=U(n)≡1。

4.刘维尔函数λ(n)的逆λ-1(n)=μ(n)λ(n)。

5.设g(n)=λ*U=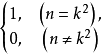，则1

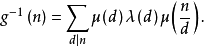
本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所