[科普中国]-三元三次不定方程

三元三次不定方程(ternary cubic indeterminate equation)是几个著名的三元三次不定方程。不定方程中比较成熟的方法是处理两个变元的不定方程，三个变元以上的高次不定方程，常常是很困难的。例如，关于三元三次不定方程x³+y³+z³=xyz无xyz≠0的整数解，曾经很长时间使数学家们束手无策，直到20世纪60年代，柯召(1960年)和卡塞尔斯(J.W.S.Cassels)(1962年)才分别独立地证明了这个问题，同时解决了谢尔品斯基(W.Sierpiski)认为是很难的一个猜想：不存在三个有理数，它们的和与积都能等于1，亦即不定方程x+y+z=xyz=1不存在有理数解1。

基本介绍设f(x，y，z)是一个整系数三元三次多项式，方程

称为三元三次不定方程，对方程(1)的解，迄今人们所知甚少。某些结果仅仅给出(1)的一些特殊情况的部分整数解，而不是全部解2。

相关结论及证明在三元三次不定方程中，最简单而且又是最重要的方程为

其中n为整数，对某些n，方程(2)有无穷多组整数解，而对另一些n，方程(2)亦可能无整数解1。例如：

1.当n=a³时，方程(2)有无数多组整数解，其解可表示为(x，y，z)=(t，-t，a)或

(9at4，3at-9at4，a-9at3)，t∈Z.

2.当n=2a3时，方程(2)也有无数多组整数解，可表示为

(x，y，z)=(a(1+6t3)，a(1-6t3)，-6at2).

3.当n≡±4(mod 9)时，方程(2)无解。这是因为

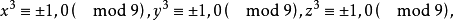所以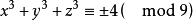，即(2)没有解。

对于方程(2)，还有一些迄今尚未解决的问题。例如，已知当n=3时，方程(2)有4个整数解为(x，y，z)=(1，1，1)，(4，4，-5)，(4，-5，4)，(-5，4，4)，尚不知道是否还有其他解。又如当n=30时，方程(2)是否有解亦不知道2。

讨论(1)的一个简单情形，不定方程

当a=b=1，c=-1时，(3)有无穷多个解。而且证明很容易，只需令x=1+ω，y=1-ω，代入z²=x³+y³-1得

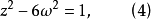方程(3)是熟知的Pell方程，有无穷多组整数解z，ω，因而a=b=1，c=-1时，(3)有无穷多组解。

另外，对三元三次不定方程ax³+ay³+bz³=bc³，abc≠0，已知在平凡解x+y=0，z=c外，还有无穷多组整数解1。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所