[科普中国]-包立方程式

泡利方程或称薛定谔-泡利方程，为描述带有自旋1/2的粒子在与电磁场相互作用下的修正方程（自旋1/2粒子例如电子）。在此之前，用以描述粒子行为的薛定谔方程则未考虑到粒子自旋的性质。其为狄拉克方程在非相对论极限下的特例，应用在粒子速度慢到相对论效应可以忽略的场合。

泡利方程是由沃尔夫冈·泡利于1927年所建构。

简介泡利方程或称薛定谔-泡利方程，为描述带有自旋1/2的粒子在与电磁场相互作用下的修正方程（自旋1/2粒子例如电子）。在此之前，用以描述粒子行为的薛定谔方程则未考虑到粒子自旋的性质。其为狄拉克方程在非相对论极限下的特例，应用在粒子速度慢到相对论效应可以忽略的场合。

泡利方程是由沃尔夫冈·泡利于1927年所建构。1

与薛定谔方程、狄拉克方程的关系泡利方程为非相对论性的量子力学方程，但其能描述自旋相关的行为，因此其具有薛定谔方程与狄拉克方程的中介角色：

常见的薛定谔方程（作用于复标量波动方程），非相对论性，也无法描述自旋。

狄拉克方程（作用于复数四分量旋量），完整地考虑了相对论效应，可描述自旋。

注意到：若磁矢势A为零，泡利方程则约化为一个在纯电势ϕ中运动的带电粒子之薛定谔方程：

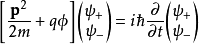
但因为泡利矩阵的存在，此方程是作用在二分量旋量上的。因此仅当磁场存在时，粒子自旋才会对粒子的运动发挥影响。1

沃尔夫冈·泡利沃尔夫冈·欧内斯特·泡利（德语：Wolfgang Ernst Pauli，1900年4月25日－1958年12月15日），奥地利理论物理学家，是量子力学研究先驱者之一。1945年，在爱因斯坦的提名下，他因泡利不相容原理而获得诺贝尔物理学奖。泡利不相容原理涉及自旋理论，是理解物质结构乃至化学的基础。1

自旋1/2在量子物理中，自旋½表示一粒子所具有的内禀角动量（自旋）为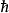，是约化普朗克常数，其中包括了电子、质子、中子、中微子与亏子(夸克)。自旋-½粒子在量子统计上属于费米子，并遵守泡利不相容原理。

对自旋½粒子进行自旋性质的量子测量会得到两个值。有两个结果肇因于所存有的矢量空间的维度。自旋½粒子的自旋量子态可以用一种两个维度的复数值矢量来描述，称之为二元旋量。利用这种表示法，量子力学中的算符可写成2乘2(2 x 2)的复数厄米矩阵。1

薛定谔方程在量子力学中，薛定谔方程（Schrödinger equation）是描述物理系统的量子态怎样随时间演化的偏微分方程，为量子力学的基础方程之一，其以发表者奥地利物理学家埃尔温·薛定谔而命名。关于量子态与薛定谔方程的概念涵盖于基础量子力学假说里，无法从其它任何原理推导而出。

在经典力学里，人们使用牛顿第二定律描述物体运动。而在量子力学里，类似的运动方程为薛定谔方程。薛定谔方程的解完备地描述物理系统里，微观尺寸粒子的量子行为；这包括分子系统、原子系统、亚原子系统；另外，薛定谔方程的解还可完备地描述宏观系统，可能乃至整个宇宙。

薛定谔方程可以分为“含时薛定谔方程”与“不含时薛定谔方程”两种。含时薛定谔方程与时间有关，描述量子系统的波函数怎样随着时间而演化。不含时薛定谔方程则与时间无关，描述了定态量子系统的物理性质；该方程的解就是定态量子系统的波函数。量子事件发生的概率可以用波函数来计算，其概率幅的绝对值平方就是量子事件发生的概率密度。

薛定谔方程所属的波动力学可以数学变换为维尔纳·海森堡的矩阵力学，或理察·费曼的路径积分表述。薛定谔方程是个非相对论性方程，不适用于相对论性理论；对于相对论性微观系统，必须改使用狄拉克方程或克莱因-戈尔登方程等。2

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所