[科普中国]-简化剩余系

简化剩余系(reduced residue system)也称既约剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。例如，模5的一个简化剩余系是1，2，3，4，模10的一个简化剩余系是1，3，7，9，模18的一个简化剩余系是1，5，7，11，13，171。

基本介绍简化剩余系是一种特殊的完全剩余系，在模m的每个互素剩余类Cr(0≤r≤m-1，(r，m)=1)中任取一数ar，则所有的数ar(0≤r≤m-1，(r，m)=1)所组成的集，称为模m的一个简化(互素)剩余系。有无穷多个简化剩余系，其一般形式为ar=qrm+r，0≤r≤m-1，qr可任意选取，qr=0是最常用的取法，这时ar=r，(r，m)=1，0≤r≤m-1。当m=p为素数时，最重要的简化剩余系为：1，2，…，p-1，模m的简化剩余系由φ(m)个整数组成，且任意φ(m)个整数组成模m的一组简化剩余系的充分必要条件是这些数与m互素，并对模m两两不同余2。

简化剩余系的性质简化剩余系有下列性质：

1.设m为自然数，k，l为任意整数，(k，m)=1，则当x通过m的简化剩余系时，kx+lm亦通过模m的一组简化剩余系，例如x与m-x同时通过模m的简化剩余系。

2.设m1，m2为自然数，(m1，m2)=1，则当x，y分别通过模m1，m2的简化剩余系时，m2x+m1y通过模m=m1m2的简化剩余系。

3.设m1，m2，…，mk是k个两两互素的自然数，x1，x2，…，xk分别通过模m1，m2，…，mk的简化剩余系，则M1x1+M2x2+…+Mkxk通过m=m1m2…mk的简化剩余系，其中m=miMi(i=1，2，…，k)。

4.若m是大于1的正整数，a为整数，(a，m)=1，x通过模m的简化剩余系，则。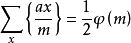

缩同余类的概念在近世代数中有应用，若A是模m的缩同余类，把满足Ax=C1的惟一的缩同余类x表示成A-1，则Ax=B的惟一解可记为x=BA-1=A-1B(或写成B/A)，即只有模m的缩同余类才能作分母，于是在模m的缩同余类之间可以定义除法运算。特别地，当m为素数p时，除了C0之外，其他p-1个同余类都是缩同余类。因此，加减乘除四则运算在模p同余类集合中都是可以进行的(当然C0不能作分母)，这样的集合称为“域”，模p的p个缩同余类构成了有限域，这为近世代数提供了有限域的实例2。

简化剩余系的构造简化剩余系的构造是对简化剩余系的一种刻画，指用原根表达简化剩余系。若 ɡ是模m的原根，则模m的简化剩余系可表为：1， ɡ， ɡ2，…， ɡφ(m)-1。在一般情况下，正整数m不一定存在原根。

关于简化剩余系的构造有如下定理：

1.若m=pα(素数p≥2)存在原根 ɡ，则模m的简化剩余系为： ɡº， ɡ¹， ɡ²，…， gφ(m)-1。

2.若m=2α，α≥3，这时m无原根，则5和3对2α的阶为2α-2，且

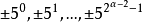及

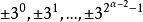均构成模m=2的一个简化剩余系。

3.若正整数m的标准分解式为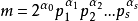， g1， g2，…， gs分别为模m的原根，则对任给一组数(r-1，r0，r1，…，rs)，0≤r-1