[科普中国]-仿射密码

仿射密码为单表加密的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。

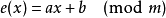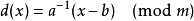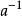介绍仿射密码是一种替换密码。它是一个字母对一个字母的。它的加密函数是，其中a和b互质，m是字母的数目。解码函数是，其中是a在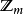群的乘法逆元。1

仿射密码为单表加密的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。 其仍有所有替代密码之弱处。所有字母皆借由方程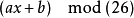加密，b为移动大小。

在仿射加密中，大小为m之字母系统首先对应至0..m-1范围内之数值， 接着使用模数算数来将原文件中之字母转换为对应加密文件中的数字。 单一字母的加密函数为

取余m为字母系统大小且a和b为密码关键值。a之值必须使得a与m互质。解密方程为

此处满足等式。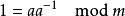

a之乘法逆元素仅存在于a与m互质条件下。 由此，没有a的限制，可能无法解密。 易知解密方程逆于加密方程。

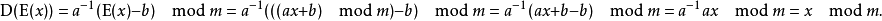
缺点因为仿射密码仍为单字母表密码, 其依旧保留了该类别加密之弱处。当a=1，仿射加密为凯撒密码，因该加密方程可简化为线性移动。 考虑加密英文。(即：m=26)，不计26易凯萨密码，总共有286非易仿射密码。此数值是由于小于26之数中有12数与26互质。a 的每个值可有26互异之加法移动(b之值)；因此，共有 12*26 或 312 可能之关键值。 因为密码缺少复杂性，根据柯克霍夫原则，这套系统是不安全的。

此密码之首要弱处为，如果密码学家可发现(如频率分析, 暴力破解, 臆测或任何其他方法) 加密文件两字元之原文，则关键值可透过解一方程组得到。 由于我们知道a及m互质，这个事实可被用于快速破解密码。

仿射密码中同种的转换使用于线性虚拟随机产生器， 为虚拟随机数产生器其中一种。 此产生器不为安全加密虚拟随机数产生器，因仿射密码不安全。

范例在以下一加密一解密的例子中，字母为从A至Z，且在表格中都有对应值。

|| ||

加密在加密范例中，,使用前述表格中各字母对应之数值可知欲加密的原文件为 "AFFINE CIPHER" ，a对应5，b对应 8，而m对应26 （因共使用26字母）。a的所有可能值有 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 与 25。 若a不等于 1，b之值可随机选定， 所以，此加密范例的函数为。加密讯息的首步即为写出每个字母的数字值。

|| ||

现在，取x各值并解等式的第一部分，(5x+8)。 得出各字母对应 (5x+8)的值后，取其对26的余数。以下表格为加密的首四步骤。

|| ||

加密讯息的最后一步，为查表求得对应字母的数值。 在此范例中，加密文本应为 IHHWVCSWFRCP。 以下表格显示仿射加密一讯息的完整表格。

|| ||

解密于此解密范例中，欲解密之加密文件来自加密范例 。其解密方程为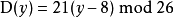，经过计算，a-1为 21，b为8，m为 26。伊始之时，写下加密文件中对应各字母之数值，如以下表格所示：

|| ||

下一步，计算21(y-8)，再取结果除以26的余数。以下表格显示两者计算后的结果。

|| ||

解密的最后一步，借由表格将数值转回字母。解密的原始文件为 AFFINECIPHER。 以下为完成解密后的表格：

|| ||

全数字母加密为求加解密更快速，可加密全数字母以将原文件之字母一对一对应至加密文件。此范例中，一对一映射如下：

|| ||

程式实例用Python编程语言，以下代码可用于加密罗马字母A至Z。2

# 列印仿射密码的字母表。# a必须与m互质 def affine(a, b): for i in range(26): print chr(i+65) + ": " + chr(((a*i+b)%26)+65)# 调用函数的例子 affine(5, 8)或者以Java作例:

public void Affine(int a, int b){ for (int num = 0; num