[科普中国]-丛内图形

丛内图形是一种空间图形。对于中心直线丛O，如果在空间图形F上，任取异于丛心O的点A，若射线OA上的所有点都在F上，则图形F称为丛O内图形。对于平行直线丛，具备下述性质的空间图形F称为丛内图形：在F上任取一点A，直线AB若平行于丛内直线，则AB上所有点都在F内。

简介丛内图形是一种空间图形。

直线丛所有有三个参数的直线的集合组成直线丛。直线丛按下述意义填满了整个空间或空间的一部分：过其中每一点都有无数多条直线属于此集合，直线丛中经过某点的直线组成以该点为顶点的锥面。若锥面退化成为平面上的线束，则直线丛叫做线性的。

中心直线丛的方程经过一个定点的空间所有直线的集合称为一个中心直线丛，它们的公共点称为直线丛的中心；平行于一条固定直线的空间所有真线的集合称为平行直线丛，以已给点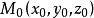为中心的直线丛方程可以写成

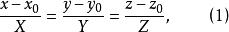其中X，Y，Z不同时为零，称为直线丛的参数；当它们取不同比值时，得直线丛里不同直线，所以起作用的参数实际上只有两个。

平行直线丛的方程平行于矢量(X，Y，Z)的平行直线丛的方程也可以写成(1)的形状，但此时X，Y，Z为已给，改变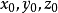的值，可以得不同直线。当然，丛里每条直线上的任意两点决定同一直线。

假设Z≠0，则平行直线丛的方程可以写成

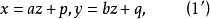其中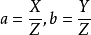为已知，不同的数偶p, q对应不同的直线，p，q是平行直线丛(1')的参数。1

分类对于中心直线丛O，如果在空间图形F上，任取异于丛心O的点A，若射线OA上的所有点都在F上，则图形F称为丛O内图形。中心直线丛的丛内图形如:过丛心O的直线、平面；棱过丛心O的二面角；顶点在丛心O的多面角、圆锥等。

属于丛O的丛内图形的集合与以O为球心的球面图形的集合，可建立一一对应，即一个丛内图形对应于它与球面相截、截出的球面图形。例如，与上列丛内图形相对应的球面图形是：直径两端点、大圆、球面二角形、球面多边形、小圆等。

对于平行直线丛，具备下述性质的空间图形F称为丛内图形：在F上任取一点A，直线AB若平行于丛内直线，则AB上所有点都在F内。平行直线丛的丛内图形如：平行于丛内直线的直线或平面，棱平行于丛内直线的二面角，母线平行于丛内直线的圆柱面等。2

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所