[科普中国]-球面小圆

球面小圆(spherical small circle)简称小圆，用不通过球心的平面去截球面，所截得的曲线是一个圆，称为这个球面的小圆。球面小圆上的任一段弧称为球面小圆弧，简称小圆弧，球面上任意两点间的球面小圆弧之长不是这两点间的球面距离1。

基本介绍球面小圆是一条与球面有关的封闭曲线，指球面和不通过球心的平面的交线，如图1中的⊙O₁。球面小圆圆心与球心的连线，垂直于球的小圆面。在半径为R的球面中，圆心距球心为d的球面小圆的半径为

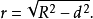
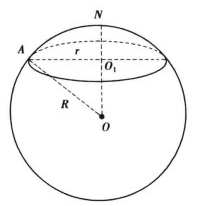
球面圆是球面几何的基本概念之一，是球面在空间中与平面相交时的交线圆，包括平面通过球心时交成的球面大圆和平面不通过球心时与球面相交而成的球面小圆。垂直于球面圆所在平面的直径的两个端点(对径点)称为球面圆的球面中心，亦称为球面圆的极。球面大圆的圆弧、优弧、劣弧、余弧、共轭弧依次称为球面大圆弧、大圆优弧、大圆劣弧、余大圆弧、共轭大圆弧。当提到连结球面上非对径的两点的大圆弧时，通常指大圆劣弧，此大圆弧的长度称为此两点间的球面距离。因为球面上非对径的两点与球心不共线而决定一个平面，这两点就在由此平面与球面相交的惟一大圆上，所以上述球面距离的定义适用于球面上非对径的任意两点，至于球面的两个对径点，自然地以半大圆弧的长度作为它们的球面距离，球面圆的球面中心与球面圆上的点的球面距离相等，即球面圆是球面上与一个定点的距离等于定值的点的轨迹，此定点即球面圆的球面中心或极，这个定值称为球面圆的球面半径，亦称为球面圆的角半径、弧半径或极距，球面大圆的球面半径等于一象限弧，球面小圆与两个球面中心(极)相应有小于和大于一象限弧的两个球面半径，球面半径小于一象限弧的极称为近极，另一个称为远极，由于球面小圆的球面中心通常是指离该圆所在平面的距离较近的那个近极，因此，球面小圆的球面半径通常指小于一象限弧的那一个1。在空间直角坐标系中，球心为点(a，b，c)半径为R的球面的方程是1

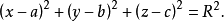
例题解析【例1】球面上有三个点，其中任意两个点的球面距离都等于大圆周长的1/6，经过这三个点的小圆周长为4π，那么这个球的半径为( )。

A.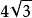 B.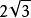 C.2 D.3

分析 设该球球心为O，半径为R，球面上三点为A，B，C，则依据题意知O-ABC是正三棱锥，侧棱长即为球的半径R。

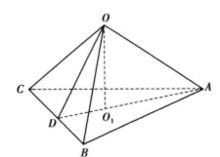
如图2，由已知得，两条侧棱的夹角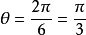 ，正三角形ABC外接圆半径 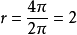。在三角形ABC中，由正弦定理得:AB=2r sin 60°=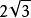。故选B2。

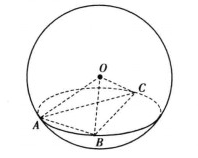
【例2】如图3，A,B,C是表面积为48π的球面上三点，AB =2,BC =4,∠ABC =60°，O为球心，则直线OA与截面ABC所成的角是( )。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所