[科普中国]-三角形二次元素

三角形二次元素是三角学的基本概念之一，指与三角形有关的图形面积，如三角形的面积、外接圆的面积及内切圆的面积等。为了提高三角形线性元素的精度，可以通过在其上增加节点并相应地提高插值多项式的次数的办法，构造三角形二次元素、三角形三次元素等。

简介三角形二次元素是三角学的基本概念之一，指与三角形有关的图形面积，如三角形的面积、外接圆的面积及内切圆的面积等。1

计算公式三角形面积1.已知三角形底a，高h，则 。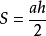

2.（海伦公式）已知三角形三边a,b,c，则

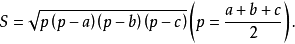
3.已知三角形两边a,b，这两边夹角C，则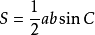 ，即两夹边之积乘夹角的正弦值。

4.设三角形三边分别为a、b、c，内切圆半径为r，则三角形面积= 。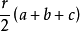

5.设三角形三边分别为a、b、c，外接圆半径为R，则三角形面积= 。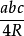

6.行列式形式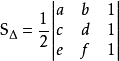： 为三阶行列式，此 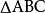在平面直角坐标系内 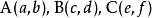，这里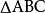 选取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小。该公式的证明可以借助“两夹边之积乘夹角的正弦值”的面积公式1。

7.海伦——秦九韶三角形中线面积公式：(其中Ma，Mb，Mc为三角形的中线长。)

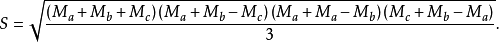
8.根据向量求面积：

其中，(x1,y1,z1)与(x2,y2,z2)分别为向量AB与AC在空间直角坐标系下的坐标表达，即：向量临边构成三角形面积等于向量临边构成平行四边形面积的一半。

三角形外接圆的面积由正弦定理可得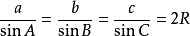，其中R为外接圆半径，已知外接圆半径易得外接圆面积。

三角形内切圆的面积直角三角形的内切圆半径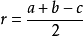（其中a,b为直角边，c为斜边），已知内切圆半径易得内切圆面积。

一般三角形的内切圆半径为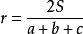，S是三角形的面积公式，已知内切圆半径易得内切圆面积。

应用为了提高三角形线性元素的精度，可以通过在其上增加节点并相应地提高插值多项式的次数的办法，构造三角形二次元素、三角形三次元素等。2

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所