有效估计值是指在诸多无偏估计值中具有最小方差的无偏估计值,是在无偏估计基础上的一种估计方法。
前提由于有效估计的基础上的一种估计方法,所以在介绍有效估计之前,最小方差无偏估计的概念知识需要向大家提前介绍。
无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值,则称此此估计量为被估计参数的无偏估计,即具有无偏性,是一种用于评价估计量优良性的准则。无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。无偏估计常被应用于测验分数统计中1。
而具有最小方差的无偏估计的判别方法如下:
设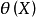 是
是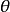 的一个无偏估计,
的一个无偏估计,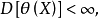 若对任何满足条件:
若对任何满足条件: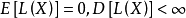 的统计量
的统计量 ,有
,有
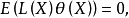
则无偏估计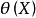 是
是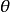 的最小方差无偏估计。
的最小方差无偏估计。
定义由样本值求得的估计值,方差越小,估计值接近待估参数的概率越大,种特性称为估计的有效性2。
设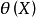 是
是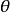 的一个无偏估计,若
的一个无偏估计,若

则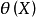 是
是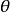 的有效估计。
的有效估计。
因为多次测定的平均值比单次测定值具有更好的精密度,因此,用平均值要比单次测定值xi作为总体均值μ的估计值更有效。在正态分布中,不知总体分布时,均值仍然可以作为分布的无偏估计值,但不是有效的。有结果(Gauss-Markov Theorem)指向这个结论,均值比总体均值μ的其他线性无偏估计值拥有更小的方差。
性质(1)设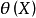 是
是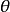 的任一无偏估计,称
的任一无偏估计,称
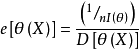
为估计量的效率,且显然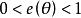 。
。
(2)如果无偏估计量的效率满足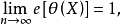 则称
则称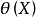 为渐进有效估计。
为渐进有效估计。
(3)如果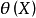 为有效估计,则它也是最小方差无偏估计,但反之却不成立。
为有效估计,则它也是最小方差无偏估计,但反之却不成立。
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国