[科普中国]-湍流扩散系数

基于Taylor(1921)提出的湍流扩散理论，可计算不同时间尺度的湍流扩散系数，可给出湍流扩散系数随时间尺度的变化关系。海域湍流扩散系数不能用一常量来描述，它是随时间尺度而变化的量。可通过相关公式来计算海域湍流扩散系数和云系湍流扩散系数。

1、基本理论湍流扩散系数的概念，源自于Fick的分子扩散理论。利用与分子扩散系数相似的表达式来定义湍流扩散系数，其表达式为：

式中Kx为湍流扩散系数，c为时均浓度；μ‘、c'分别为流速和浓度的脉动值。

根据这个概念，Taylor于1921年提出了利用定点连续测流资料，计算湍流扩散系数的公式的表达式为：

式中μL'、VL‘分别为x方向和y方向的拉格朗日湍流速度分量；RLx、RLy分别为x、y方向拉格朗日湍流的自相关函数。

假定拉格朗日流与欧拉流的统计性质相似，并且，改变一定的时间长度，拉格朗日湍流自相关函数与欧拉湍流自相关函数相等。基于这个假定，便可完成欧拉流同拉格朗日流的转换，即：

式中μE'、VE‘分别为x、y方向欧拉湍流的速度分量；RE为欧拉自相关函数；β为一参数。

由式(4)可得

将式(3)、(5)代入式(2)中有

比例参数β的值在这里取为1.0。欧拉湍流自相关函数由下式计算:

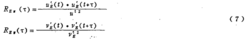
2、海域湍流扩散系数海域湍流扩散系数可以根据现场的瞬时点源扩散实验、连续点源扩散实验、浮标群扩散实验来确定，也可以利用定点连续卖测海流资料来推算。前三种方法比较直观地显示了污染物在海域中扩散的实际情况，但在实际应用中，实施起来比较困难，花费较大。利用定点连续实测资料，进行扩散系数推算，则比较简单易行，应用比较普遍。

对特定海区，湍流扩散系数不是一个绝对常量，而是一个相对于时间尺度而变化的量。在实际应用中，要根据不同的研究对象的尺度来选取湍流扩散系数。对于时空尺度变化不大的研究对象，可以取湍流扩散系数为常数；而对于时空尺度变化较大的研究对象，则需考虑扩散系数相对于时空尺度的变化关系。21

3、云系湍流扩散系数理论上研究湍流扩散的是半经验混合长输送理论和统计理论。在半经验混合长理论中，湍流场中平均浓度C满足方程：

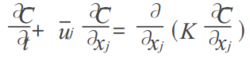
式中K为湍流扩散系数。在近地层中，有比较成熟的K理论，但应用于整个对流层中，利用常规气象资料计算K的公式还不多见。

里查逊数

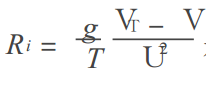
是表征大气垂直稳定度的量，它综合考虑了大气热力和动力因子。利用Ri计算公式中的各种物理量，可确定计算湍流扩散系数的公式为：

式(1)中，u为风速，U为平均风速的垂直梯度，单位ms-1km-1，Vm=6.5℃km-1是湿绝热温度递减率，V为温度递减率，以℃km-1表示，T为绝对温度，g为重力加速度。式(1)适应于有云大气，对于无云大气，Vm变换为干绝热温度递减率Vd，Vd=9.8℃km-1。3

本词条内容贡献者为:

黎明 - 副教授 - 西南大学