[科普中国]-晶体场效应

晶体场理论是计算离子能级的一种有效方法，在物理，化学，矿物学，激光光谱学以及顺磁共振中有广泛应用。

基本思想认为中心离子的电子波函数与周围离子（配位子）的电子波函数不相重叠，因而把组成晶体的离子分为两部分：基本部分是中心离子，将其磁性壳层的电子作量子化处理；非基本部分是周围配位离子，将其作为产生静电场的经典处理。配位子所产生的静电场等价为一个势场——晶体场1。

晶体中的晶体场效应a.晶体场对磁性离子轨道的直接作用引起能级分裂使简并度部分或完全解除，导致轨道角动量的取向处于被冻结状态。

b.晶体场对磁性离子自旋角动量的间接作用。通过轨道与自旋耦合来实现。常温下，晶体中自旋是自由的，但轨道运动受晶体场控制，由于自旋－轨道耦合和晶体场作用的联合效应，导致单离子的磁各向异性。

晶体场劈裂作用考虑到晶体场与L-S 耦合作用，晶体系统的哈密顿量为：

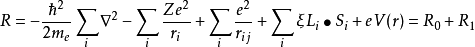
等式中间第一项为第i个电子的动能，第二项为电子势能，第三项为原子内电子的库仑相互作用，第四项为S-L轨道相互作用，第五项为中心离子与周围配离子产生的晶场间相互作用。

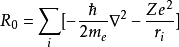
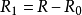(微扰哈密顿量)

采用简并态微扰法可计算系统的微扰能量，为此，须求解方程：

1. 弱晶场

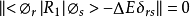
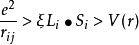
与自由原子（离子）一样，满足洪特规则。

稀土金属及其离子属于此

2. 中等晶场

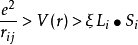
仍满足洪特规则，但晶体场V(r)首先对轨道能量产生影响，即能级分裂，简并部分或完全消除。

含3d电子组态的离子的盐类属于此

对于3d电子， l=2，角动量可有2l+1 =5个不同取向，由此形成五重简并能级如下（能量由n决定）：

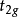项（三重简并）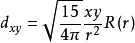

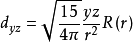
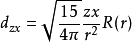
eg(2)项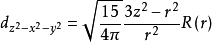

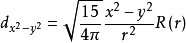
注： R(r)为归一化的径向波函数

选用Richardson等人的近似， Hartfree-Fock解析波函数：

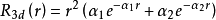
使3d电子的简并能级分裂的方法：
a. 外加磁场
不同取向的角动量对应不同的磁矩（大小、方向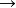） 不同的磁矩对确定方向的H有不同的位能 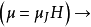磁场使原来简并的能级分裂为五个不同的能级1。

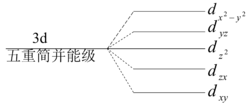
b. 将3d电子置于晶场中

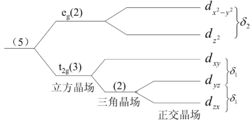
由于eg的两个轨道正对近邻离子，而t2g的三个轨道指向两个近邻离子的间隙区域，因而有能级间能量差关系为δ1