[科普中国]-三角形线性元素

三角形线性元素是三角学的基本概念之一指与三角形有关的线段，如三角形的周长、高、中线、角平分线、外接圆半径、内切圆半径及旁切圆半径等。

简介三角形线性元素是三角学的基本概念之一，指与三角形有关的线段，如三角形的周长、高、中线、角平分线、外接圆半径、内切圆半径及旁切圆半径等。1

在用有限元素法求解二维问题（包括平面问题及轴对称问题）时，最简便可行的方法是：将求解区域进行三角形有限元素分割，取三角形元素的顶点为节点，在每个三角形元素上利用三个顶点上的函数值进行线性插值，并在此基础上将所考察的泛函离散化，最后引出有限元素法的计算格式而求解。象这样的元素，称为三角形线性元素。

计算公式周长若三角形的周长用l表示，则

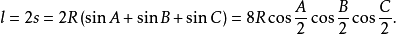
高线长若三角形的三边a,b,c边上的高线长分别用ha，hb，hc表示，则：

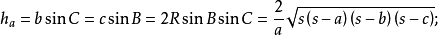
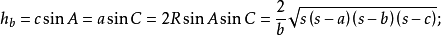
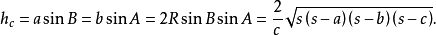
中线长若三角形的三边a,b,c边上的高线长分别用ma，mb，mc表示，则：

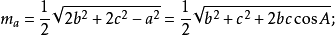
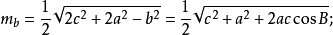
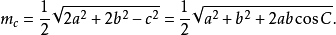
内角平分线长若三角形的三内角A，B，C的角平分线长分别用ta，tb，tc表示，则：

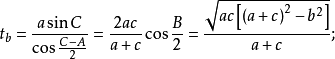
外角平分线长三角形外角平分线是指内角对边的延长线和该内角邻接的外角平分线的交点到该内角顶点线段的长。当无交点时外角平分线长不存在。若三角形的三内角A，B，C的角平分线长分别用ta’，tb’，tc’表示，则：

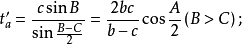
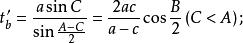
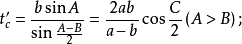
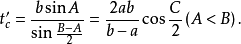
内切圆半径若三角形的内切圆半径用r表示，则

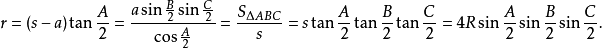
外接圆半径若三角形的外接圆半径用R表示，则

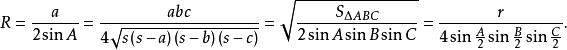
旁切圆半径若三角形的三边a,b,c边上的旁切圆半径分别用ra，rb，rc表示，则：

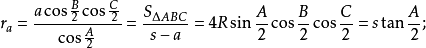
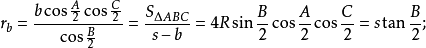
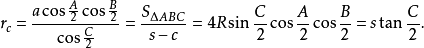
应用在计算实践中可以发现，采用三角形线性元素是比较方便的，且能比较灵活地适应不规则的几何形状，因而仍不失为是一种简便有效的方法。但是，由于采用的是线性插值，精度往往不够理想，例如，在应力分析问题中，它在每个元素中的应力和应变都是常数，因而，特别在应力集中的部位，产生的误差较大；有时即使在应力集中的范围内配置极为密集的元素，仍然不能较好地反映应力集中的趋势，不能给出应力集中因子的比较正确的数值。2

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所