拉盖尔定理(Laguerre theorem)是射影几何的重要定理之一。设两条非迷向直线的交角为θ,若这两条直线与过它们交点的两条以-i,i为斜率的迷向直线所成的交比为μ,则θ=(ln μ)/2i,由拉盖尔定理可得到:两条非迷向直线垂直的充分必要条件是这两条直线与过其交点的两条迷向直线调和共轭,即μ=-1,亦即两直线垂直的充分必要条件是两直线上的无穷远点与虚圆点调和共轭。拉盖尔定理把交比与调和共轭这两个射影概念表达成角与垂直这两个度量概念,给角和垂直以射影解释,从而把欧氏几何与射影几何联系起来。拉盖尔(E.N.Laguerre)是最先探讨复射影平面理论者之一。他建立了用交比定义角的度量公式,把欧氏几何与射影几何联系起来1。
基本介绍在笛卡儿齐次坐标下,我们把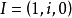 和
和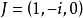 都称为圆点;过圆点
都称为圆点;过圆点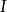 或J的直线叫做迷向直线。可以证明圆点与笛卡儿齐次坐标系的选取无关。
或J的直线叫做迷向直线。可以证明圆点与笛卡儿齐次坐标系的选取无关。
之所以把I,J称为圆点,是因为每个圆都通过这两个点。事实上,我们有如下结论。
定理1 非退化的二阶曲线是圆的充分必要条件是该二次曲线通过两个圆点。
证明: 必要性。在齐次笛卡儿坐标系下,圆的方程是
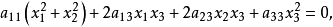 圆点
圆点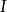 或J显然满足此方程2。
或J显然满足此方程2。
充分性。设二阶曲线
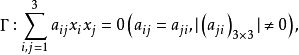 将圆点
将圆点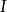 或J分别代入二阶曲线
或J分别代入二阶曲线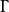 的方程,得
的方程,得
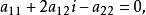 和
和
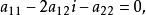 由此得
由此得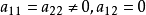 。于是
。于是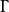 的方程为
的方程为
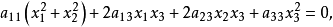
下面是重要的定理——拉盖尔(Laguerre)定理,这个定理将两直线的夹角与交比联系起来,从而为利用射影几何知识解决欧氏几何问题提供支持。
拉盖尔定理 设两条非迷向直线的夹角为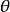 ,这两条直线与过它们交点的两条迷向直线的交比
,这两条直线与过它们交点的两条迷向直线的交比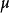 满足
满足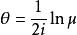 。
。
推论 两条非迷向直线垂直的充分必要条件是这两条直线与过它们的交点的两条迷向直线调和共径2。
拉盖尔定理的证明设这两条非迷向直线为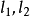 ,过这两条直线交点的两条迷向直线分别为
,过这两条直线交点的两条迷向直线分别为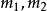 。直线
。直线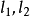 的斜率分别设为
的斜率分别设为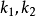 。因为过圆点J与过圆点I的迷向直线方程分别为
。因为过圆点J与过圆点I的迷向直线方程分别为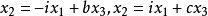 (其中b,c为复数),所以直线
(其中b,c为复数),所以直线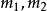 的斜率分别为-i,i。于是有2
的斜率分别为-i,i。于是有2
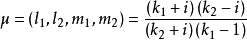
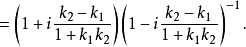 因为
因为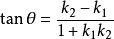 ,代人上式得
,代人上式得
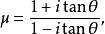 因为
因为
 于是
于是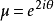 ,即
,即
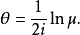
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国