[科普中国]-面对称空间图形-

面对称空间图形(space figure symmetric with respect to a plane)是一种特殊的图形，指空间图形以一个镜面反射变换为其自对称变换的图形。镜面反射变换的反射面称为图形的对称面，面对称空间图形可以不只一个对称面，面对称空间图形上任何一点关于对称面的对称点都在本图形上，且任何一双对称点的连线段被对称面垂直平分1。

基本概念如果一个图形经过平面对称后所得到的图形仍是这个图形本身，则这个图形叫做关于平面的自相对称的图形，或叫做面对称图形（如图1,2所示）。如果一个图形经过轴对称后所得到的图形仍是这个图形本身，这个图形叫做关于轴的自相对称的图形，或叫做轴对称图形，如果一个图形经过中心对称后所得到的图形仍是这个图形本身，则这个图形叫做关于中心的自相对称图形，或叫做中心对称图形，这三种图形统称为对称图****形2。

在客观实际中对称图形是一种常见的几何图形，例如自然界中的雪花和晶体、房屋建筑、桥梁、桌子、碗、茶杯等等很多是对称图形，它们既美观又实用。

|| ||

三种对称形式的关系我们可以证明三种对称形式之间有下面的关系．

定理1 如果直线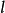和平面M垂直相交于O点，一个空间图形具有下列对称性：

1. 关于平面M对称；

2. 关于轴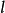对称；

3. 关于中心O对称。

中的任意两个，则它一定具有第三个。

这个定理的意思就是在一定的条件下，如果一个图形同时是两种对称图形，那么它一定是第三种对称图形2。

证明下面只证明其中的一种情况，例如如果一个空间图形关于平面M对称，且关于中心O对称，那么它一定关于直线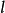成轴对称。其余情况可同理推证。

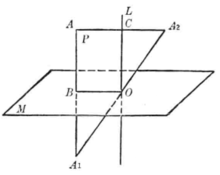
如图3中，设A是图形F上的任意一点，作A点关于平面M的对称点A'，再作A₁点关于O点的对称

点A₂，由于图形F是面对称图形，又是中心对称图形，所以A₁、A₂都在图形F上。

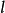∵ ⊥平面M，AA₁⊥平面M，

∴AA₁// ，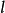

AA₁和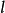确定平面P，则O点在平面P上，

∴A₁O在平面P上，A2点也在平面P上，

即A、A₁、A₂和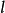都在平面P上。

连接AA2和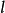交于C点，AA1与平面M交于B点，连接OB，

∵AB= A₁B，OA₁= OA₂，

∴AA₂//OB，而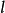 ⊥OB，

∴AA₂⊥ ，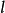

又AA₁// ，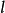

∴AC= A₂C，

∴A和A₂关于直线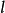成轴对称2

平面对称(镜面反射)如果图形F和F’的对应点的连线段均被某一固定平面σ垂直平分，则称图形F和F’关于平面一对称，并把从图形F到F’的变换叫做平面对称变换，简称面对称。其中，平面σ叫做对称平面，平面对称变换又叫做平面反射、镜面反射变换，简称镜面反射或平面反射。欧氏空间中的一种特殊变换，在欧氏空间中，把任一点A映成关于给定平面π对称的点A′的变换称为关于平面π的镜面反射变换，平面π称为反射平面，镜面反射是第二种正交变换，在镜面反射变换下，连结变换的每一对对应点A，A′所得到的线段都垂直于反射平面π且被π所平分，平面π上的点都是不动点，镜面反射变换在直观上相当于把平面π看做一面镜子，变换前后的对应点就好比是物与像那样，在空间直角坐标系中，若把坐标平面xOy取为反射平面，则镜面反射变换的代数表达式为1

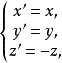其中(x，y，z)，(x′，y′，z′)分别是变换前的点与变换后它的对应点的坐标。

镜面反射亦称非特征正交变换，又称第二类正交变换，是一种特殊的正交变换。设V是欧氏空间，α是V的非零向量。对任意的β∈V，由

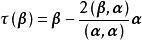决定的变换是满足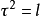的正交变换，称为由向量α决定的镜面反射，其中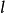为单位变换。若V是n维欧氏空间，则存在V的标准正交基，使镜面反射在此基下的矩阵为1

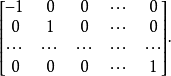
本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所