[科普中国]-含时摄动理论

在量子力学里，含时摄动理论研究一个量子系统的含时摄动所产生的效应。这理论由狄拉克首先发展成功。由于系统的含摄动哈密顿量含时间，伴随的能级与本征态也含时间。

简介在量子力学里，含时摄动理论研究一个量子系统的含时摄动所产生的效应。这理论由狄拉克首先发展成功。由于系统的含摄动哈密顿量含时间，伴随的能级与本征态也含时间。所以，不同于不含时摄动理论，含时摄动理论解析问题的目标为：

给予初始量子态，求算某个可观测量A的含时间期望值。

一个量子系统的含时间量子态，仍旧是这系统的不含时零摄动哈密顿量的本征态的线性组合。求算这系统的量子态处于某个本征态的概率幅。

第一个结果的重要性是，它可以预测由实验测量得到的答案。例如，思考一个氢原子的电子，其所在位置的 x-坐标的期望值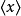，当乘以适当的系数后，给出这电子的含时间偏振。将一个恰当的摄动（例如，一个震荡的电势）作用于氢气，应用含时摄动理论，我们可以计算出交流电的电容率。详细内容，请参阅条目介电谱学(dielectric spectroscopy) 。

第二个结果着眼于量子态处于每一个本征态的概率。这概率与时间有关。在激光物理学里，假若我们知道这概率，我们就可以计算一个气体，因为含时间电场的作用，处于某个量子态的概率密度函数。这概率也可以用来计算谱线的量子增宽 (quantum broadening) 。1

哈密顿力学哈密顿力学是哈密顿于1833年建立的经典力学的重新表述，它由拉格朗日力学演变而来。拉格朗日力学是经典力学的另一表述，由拉格朗日于1788年建立。哈密顿力学与拉格朗日力学不同的是前者可以使用辛空间而不依赖于拉格朗日力学表述。关于这点请参看其数学表述。

适合用哈密顿力学表述的动力系统称为哈密顿系统。2

摄动理论 (量子力学)量子力学的摄动理论（perturbation theory）引用一些数学的微扰理论的近似方法于量子力学。当遇到比较复杂的量子系统时，这些方法试着将复杂的量子系统简单化或理想化，变成为有精确解的量子系统，再应用理想化的量子系统的精确解，来解析复杂的量子系统。微扰理论从可以获得精确解或易于得到近似解的相对简单体系出发，在这简单系统的哈密顿量(Hamiltonian)里，加上一个很弱的摄动，变成了较复杂系统的哈密顿量。假若这摄动不是很大，复杂系统的许多物理性质（例如，能级，量子态）可以表达为简单系统的物理性质加上一些修正。这样，从研究比较简单的量子系统所得到的知识，可以进而研究比较复杂的量子系统。

摄动理论可以分为两类，不含时摄动理论(Time-independent perturbation theory)与含时摄动理论(Time-dependent perturbation theory)。在不含时摄动理论中，哈密顿量的微扰项不显含时间；而含时摄动理论的摄动哈密顿量含时间，详见含时摄动理论。本篇文章只讲述不含时摄动理论。此后凡提到摄动理论，皆指不含时摄动理论。2

参阅双态系统

吸收

自发射(spontaneous emission)

受激发射(stimulated emission)

拉比问题(Rabi problem)

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所