[科普中国]-比例中项作图

比例中项作图是作两条已知线段的比例中项的简称1。作已知两条线段的比例中项的方法很多，其中常用的方法就是根据相交弦定理推论和切割线定理完成的。

基本介绍问题“作已知两条线段的比例中项”相等于问题“作一个正方形，使其面积等于已知矩形的面积?”作已知两条线段的比例中项的方法很多，其中常用的方法就是根据相交弦定理推论和切割线定理完成的。

注：当矩形的面积和正方形的面积相等时，正方形的边长是已知矩形两邻边的比例中项。

以下作图将“作已知两条线段的比例中项”问题化为“作一个正方形，使其面积等于已知矩形的面积”，其本质是一样的。“已知两条线段”即长方形的长和宽，做出来的正方形的边长即为已知两条线段的比例中项2。

作图方法作法一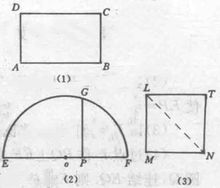

作法一：

(1)作线段EP=AB；

(2)延长EP到F，使PF= BC；

(3)以EF为直径作半圆；

(4)过点P作PG⊥EF，交半圆于点G；

(5)以GP为边长作正方形LMNT。

GP就是作已知两条线段的比例中项，正方形LMNT就是所求的正方形。

这个求已知两线段的比例中项的作图是根据相交弦定理的推论，容易证明上述作法得出的正方形LMNT的面积与已知矩形的面积相等2。

作法二设矩形ABCD的AB=a，BC=b，正方形LMNT的边长为x，则有第二种作法:见图2。

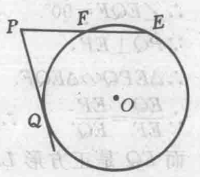
作法二：

(1)作线段PE，使PE=a；

(2)在线段PE上截取PF，使PF=b；

(3)过E、F两点任作⊙O；

(4)过点P作⊙O的切线 PQ，切点是Q；

(5)作正方形LMNT，使LM= MN=NT=TL= PQ。

则PQ就是线段a、b的比例中项，正方形LMNT，就是所求的正方形。

容易看出正方形的边长等于PQ=x，而线段PQ就是矩形的两邻边的长a，b的比例中项，根据就是切割线定理2。

作法三作法三：

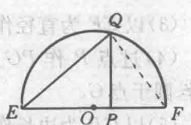
(1)作线段EF=a，如图3所示；

(2)在线段EF上截取EP，使EP=b；

(3)以EF为直径作半圆；

(4)过点P作PQ⊥EF交半圆Q。连结EQ。则EQ就是线段a、b的比例中项。

(5)以EQ为边长作正方形LMNT，则LMNT就是所求的正方形。

证明：连结FQ。

∵EF是半圆直径，

∴∠EQF=90°，

∵PQ⊥EF，

∴

∴

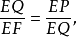
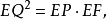
则EQ就是线段a、b的比例中项，EQ是正方形LMNT的边长，EP、EF是已知矩形ABCD的边长，因此正方形LMNT的面积等于矩形ABCD的面积2。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所