[科普中国]-封闭折线

封闭折线是一种几何图形，指一种特殊的折线。同一平面内，由不在同一直线上的几条线段顺次首尾相接所组成的图形叫作折线，如果一条折线的首尾两个端点重合，这条折线叫作封闭折线1。

基本概念不全在同一直线上的几条线段顺次首尾相接组成的图形叫做折线(如图1，图2)。各线段称为折线的边或折线的节；折线各边长之和称为折线的长；各线段的端点称为折线的顶点；相邻两个顶点称为邻顶点；不是两条线段公共端点的两个顶点都称为折线的端点；两端点重合(实际上即无端点)的折线称为封闭折线(图2)。组成折线的所有线段都在同一平面内的折线称为平面折线，否则称为空间折线。凡不相邻的两边不相交的折线称为简单折线，把一条平面简单折线的任一条边向两方延长成直线，如果能使这条折线的其他各边都在这条直线的同侧，那么这条平面折线称为凸折线，连结非封闭折线的两个端点的线段称为折线的锁线2。

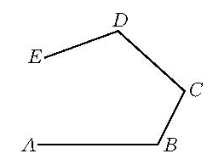
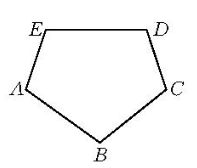
封闭折线的基本性质平面上一些线段顺次首尾相接构成的图形，称为平面折线。下面约定，任何端点不在另外的线段上，构成折线的线段称为边，线段的端点称为顶点，共边两顶点称为相邻顶点，如果折线每条边都有两条邻边，就称为封闭折线，否则，称为开折线3。

定理1 n边封闭折线有n个顶点；n边开折线有n+1个顶点。

边不相交的折线称为简单折线，简单封闭折线称为多边形，多边形将平面分为两部分，其中有限部分称为多边形的内部，不难证明有:

定理2 n边形内部可用不相交的对角线划分为n-2个三角形。

定理3 n边形内角和等于(n-2)π。

沿折线一条边经顶点A走向邻边，如向左(右)拐，A就叫作边AB的左(右)折点(图3(a))，称一端为左折点，另一端为右折点的边(图3(b))为单折边，两端均为左或右折点的边(图1(c))为双折边，且前者为左旋边而后者为右旋边，易见，封闭折线的每个顶点，分别为两邻边的左折点和右折点，封闭折线有如下特征性质，

定理4封闭折线如果有双折边,则双折边成对、左右旋边各半且相间排列。

定理5 多边形P为凸的充要条件是P的所有边均为单折边。

定理6 若封闭折线有双折边，则顶角和不定。

定理7 m阶n边星形顶角和θ(n，m) = (m+1)π3。

下面t环单折边封闭折线特征是：当沿着它的边界运动一周时，必绕某一中心旋转t圈，如下图中的折线分别1,2,3环。

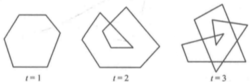
定理8 n边t环封闭折线项角和为σ(n，t) = (n-2t)π。其中，n = 3，4，5，...；t = 1，2，3，...3。

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所