沙勒定理(Chasles theorem)关于变换的著名定理,该定理断言:既非旋转也非平移的空间第一种合同变换是一个旋转与一个平移之积,且旋转轴平行于这平移的方向。简言之,既非旋转又非平移的空间第一种合同变换(运动变换)是一个螺旋运动。
历史空间位移可以分解成旋转并绕着一条线滑动的证据归功于天文学家和数学家Giulio Mozzi(1763),实际上螺旋轴在意大利传统上被称为asse di Mozzi。 然而,大多数教科书都是指Michel Chasles在1830年后的类似作品。 M. Chasles的其他几位同时代的学者在那个时期获得了相同或相似的结果,包括G. Giorgini,Cauchy,Poinsot,Poisson和Rodrigues。可以在这里找到Giulio Mozzi的1763证明及其一些历史记录。
内容当刚体移动时,它的位置与取向都可能会随着时间演进而改变。沙勒定理是欧拉旋转定律的一个推论。根据沙勒定理,刚体的最广义位移等价于一个平移加上一个旋转1。所以,刚体运动可分为平移运动与旋转运动。刚体的现在位置与现在取向可以视为是从某个初始位置与初始取向经过平移与旋转而成。
挑选刚体内部一点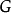 来代表整个刚体,从空间参考系
来代表整个刚体,从空间参考系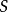 观测,点
观测,点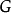 的位置就是整个刚体在空间的位置,在刚体内部任意一点
的位置就是整个刚体在空间的位置,在刚体内部任意一点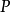 的位置
的位置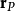 为:
为:
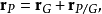 其中,
其中,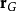 、
、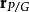 分别是点
分别是点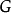 的位置、点
的位置、点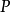 对于点
对于点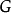 的相对位置。
的相对位置。
刚体从时间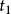 到时间
到时间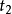 的运动,可以分为点
的运动,可以分为点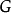 从
从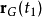 到
到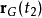 的平移运动,与位移
的平移运动,与位移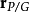 从时间
从时间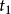 到时间
到时间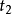 的旋转运动。点P的速度
的旋转运动。点P的速度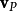 为:
为:
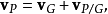 其中,
其中,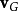 、
、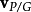 分别是点
分别是点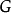 的速度、点
的速度、点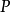 对于点
对于点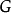 的相对速度。
的相对速度。
点P的加速度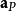 为:
为:
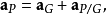 其中,
其中,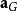 、
、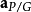 分别是点
分别是点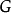 的加速度、点
的加速度、点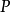 对于点
对于点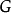 的相对加速度。
的相对加速度。
证明Michel Chasles认为刚体首先围绕穿过质心的轴旋转,然后沿任意方向平移位移。由于关于存在旋转轴的欧拉定理,可以以这种方式完成任何刚性运动。质心的位移D可以分解成平行和垂直于轴的分量。垂直(或平行)分量作用于刚体的所有点,但Michel Chasles表明,对于某些点,先前的旋转恰好具有相反的位移,因此这些点平行于旋转轴平移。这些点位于Mozzi轴上,通过螺杆运动可以实现刚性运动。
沙勒定理的另一个基本证明是E.T.Whittaker在1904年给出的2。假设A被转换为B.Whittaker建议平行于给定旋转的轴选择线AK,K是B的垂线点。适当的螺旋位移是围绕与AK平行的轴,使得K是该方法对应于欧几里德平面等距,其中旋转和平移的组成可以通过围绕适当的中心旋转来代替。在Whittaker的术语中,“围绕任何轴的旋转相当于围绕与其平行的任何轴的相同角度的旋转,以及在垂直于轴的方向上的简单平移。”
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国