[科普中国]-确定有限状态自动机最小化

在自动机理论（计算机科学的一个分支）中，确定有限状态自动机最小化是将给定的确定有限状态自动机（DFA, Deterministic Finite Automaton）改造为等价且拥有最少状态的DFA的过程。这里，两个DFA等价意味着他们识别相同的正则语言。

最小DFA对于每个正则语言，都存在一个最小自动机接受它，即一个有着最小状态数目的DFA，且这个DFA是唯一的（除去状态命名不同的差别）。最小DFA保证了其在模式匹配等计算应用中开销的最小。

在不影响原始DFA所接受语言的情况下，有两类状态可以被移除或合并，以实现最小化过程。

不可达状态指DFA在任意输入串下都无法达到的状态。

等价状态指在同一输入串下不产生区别的状态。

DFA最小化通常要经历三个步骤，分别对应于相关状态的移除或合并。因为等价状态的消解开销高昂，通常会将其放到最后一步。1

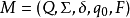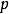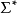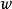不可达状态DFA 的状态 是不可达的，若不存在 上的串 ，使得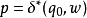 。可达状态可以用如下算法来找到：

let reachable_states := {q0};let new_states := {q0};do { temp := the empty set; for each q in new_states do for each c in Σ do temp := temp ∪ {p such that p = δ(q,c)}; end; end; new_states := temp \ reachable_states; reachable_states := reachable_states ∪ new_states;} while (new_states ≠ the empty set);unreachable_states := Q \ reachable_states;将不可达状态从DFA中移去并不会影响其接受的语言。2

等价状态Moore算法Moore DFA最小化算法由Edward F. Moore(1956)给出。与 Hopcroft 算法类似地，它维护一个划分，且这个划分的初值为接受和拒绝状态的划分，并同样反复细化直至无法继续细化。在每一步中，它都会用s+ 1个划分的最粗公细化(coarsest common refinement) 来替代当前的划分，这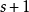 个划分中的一个是当前划分，其他的 个则是当前划分在转移函数和在所有输入符号下的原象。当这一操作无法改善当前划分时，算法即停止。这个算法在最坏情况下的复杂度是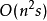 ：算法的每个步骤都需要 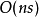，这是基数排序一个变种用以重排状态的复杂度，状态重排使得新划分下同一集合中状态的编号顺序是接连的。又，最多会有 轮，因为除最后一轮外，每轮都使得划分中的集合数目增加。在Moore算法下导致最坏情况的DFA最小化问题实例和Hopcroft算法是相同的。算法的轮数会比 小得多，所以平均上（ 是常数），其性能可达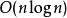 甚至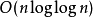 ，结果取决于建模平均情况行为的自动机随机选取分布方式。1

Brzozowski算法Brzozowski (1963) 注意到，将DFA的边反转将产生一个原语言反序的非确定有限状态自动机(NFA)。再将这个NFA用标准的幂集构造法（只构造转换后DFA的可达状态）转换为DFA，就会产生原语言反序的最小DFA。重复反转操作，就可以得到原语言的最小DFA。Brzozowski算法在最坏情况下的复杂度是指数的，因为存在这样的正则语言，其反序的最小DFA的规模是原语言DFA规模的指数大。但通常来说这个算法比最坏情况表现得要好。1

NFA最小化以上的步骤都对DFA有效，可是划分的方法并不适用于非确定有限状态自动机(NFA)。虽然穷举搜索可以最小化NFA，但并没有一个多项式时间的算法可以完成该过程，除非P=PSPACE（计算复杂性理论中的一个未解决问题，一般认为很可能P≠PSPACE）。然而的确存在比暴力搜索可能更加有效的NFA最小化算法。1

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所